Pascal-like Triangles Mod k

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
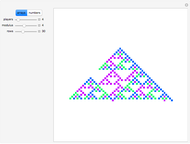
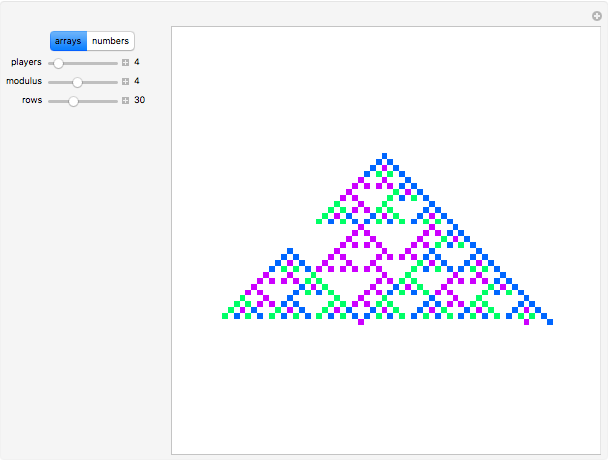
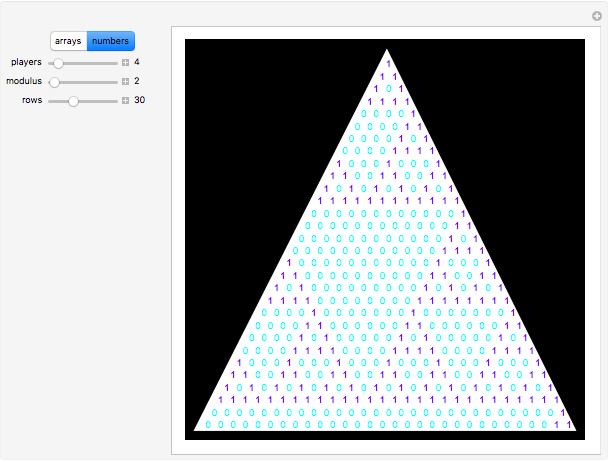
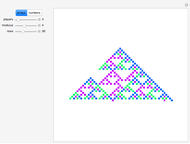
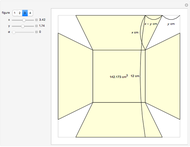
This Demonstration shows Pascal-like triangles reduced modulo  , where
, where  can vary between 2 and 7. These arrays are made from the probabilities of winning a
can vary between 2 and 7. These arrays are made from the probabilities of winning a  -player game described in Details.
-player game described in Details.
Contributed by: Hiroshi Matsui, Toshiyuki Yamauchi, Daisuke Minematsu, and Ryohei Miyadera (September 2007)
Open content licensed under CC BY-NC-SA
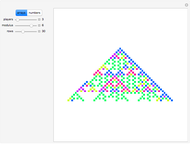
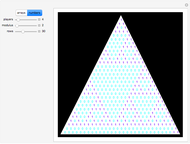
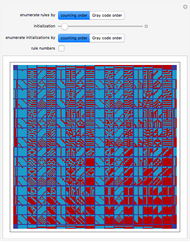
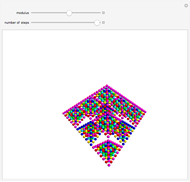
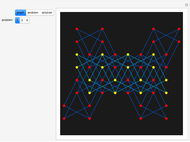
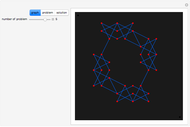
Snapshots
Details
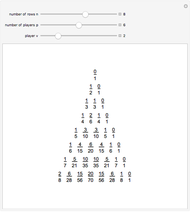
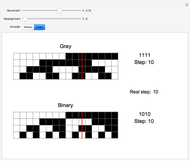
Besides the colored pixels, you can also see numbers for the Pascal-like triangles reduced modulo  . Please see the third snapshot.
. Please see the third snapshot.
Let  ,
,  ,
,  be fixed natural numbers such that
be fixed natural numbers such that  . There are
. There are  players seated in a circle. The game begins with the first player. Proceeding in order around the circle, a box of cards is passed from hand to hand. The box contains
players seated in a circle. The game begins with the first player. Proceeding in order around the circle, a box of cards is passed from hand to hand. The box contains  red cards and
red cards and  white cards. A player draws a card when the box is received. Once a card is drawn, it will not be returned to the box. If a red card is drawn, the player loses and the game ends. Let
white cards. A player draws a card when the box is received. Once a card is drawn, it will not be returned to the box. If a red card is drawn, the player loses and the game ends. Let  be the probability of the
be the probability of the  player losing the game. Then for fixed numbers
player losing the game. Then for fixed numbers  and
and  with
with  , the list
, the list  forms a Pascal-like triangle.
forms a Pascal-like triangle.
The denominators of the list form Pascal-like triangles, and these triangles, reduced modulo  , are displayed. These triangles depend on the number
, are displayed. These triangles depend on the number  of players. To make the situation simple,
of players. To make the situation simple,  .
.
If you want to know the mathematical background of the game, see R. Miyadera, T. Hashiba, Y. Nakagawa, T. Yamauchi, H. Matsui, S. Hashiba, D. Minematsu, and M. Sakaguchi, "Pascal-like Triangles and Sierpinski-like Gaskets," Visual Mathematics: Art and Science Electric Journal of ISIS-Symmetry [online], 9(1), 2007.
Because of the Pascal-like property, the triangles can be made by a kind of cellular automaton that has a kind of boundary condition.
Permanent Citation