The Josephus Problem in Both Directions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
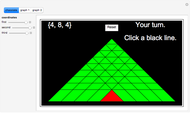
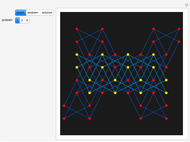
The classical version of the Josephus problem counts off  uneliminated people arranged in a circle and eliminates the
uneliminated people arranged in a circle and eliminates the  person. The process continues until only one person is left.
person. The process continues until only one person is left.
Contributed by: Hiroshi Matsui, Toshiyuki Yamauchi, Daisuke Minematsu, Soh Tatsumi, Masakazu Naito, Takafumi Inoue and Ryohei Miyadera (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
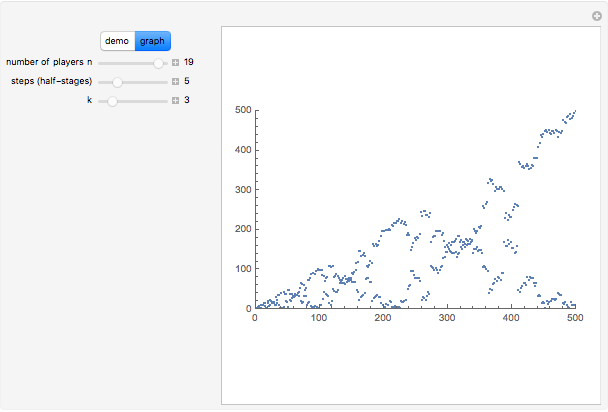
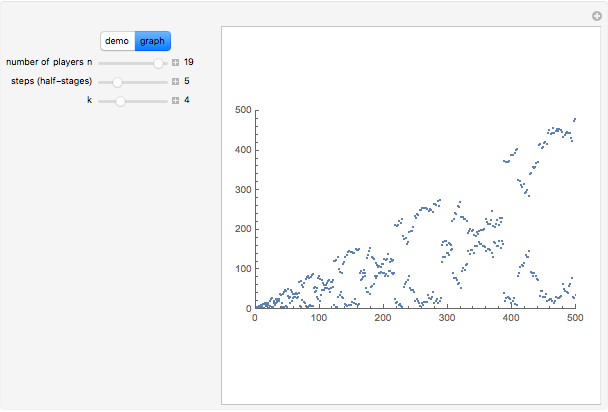
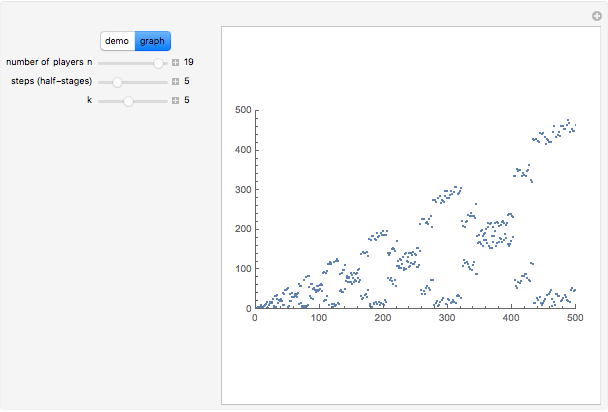
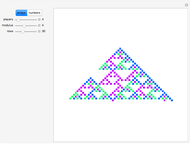
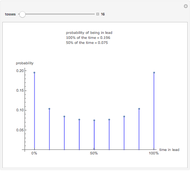
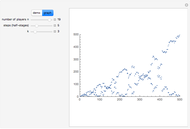
If you look at the graph of the list  , you will discover a very interesting fact: the graph is self-similar, a fractal. To prove that the graph is indeed a fractal, you need to find recursive relations for
, you will discover a very interesting fact: the graph is self-similar, a fractal. To prove that the graph is indeed a fractal, you need to find recursive relations for  . The authors are going to publish their research about the self-similarity of this graph in Kokyuroku at the Research Institute of Mathematical Science at Kyoto University. As to the other variants of the Josephus Problem, see S. Hashiba, D. Minematsu, and R. Miyadera, "How High School Students Can Discover Original Ideas of Mathematics Using Mathematica", Mathematica in Education and Research, 11(3), 2006.
. The authors are going to publish their research about the self-similarity of this graph in Kokyuroku at the Research Institute of Mathematical Science at Kyoto University. As to the other variants of the Josephus Problem, see S. Hashiba, D. Minematsu, and R. Miyadera, "How High School Students Can Discover Original Ideas of Mathematics Using Mathematica", Mathematica in Education and Research, 11(3), 2006.
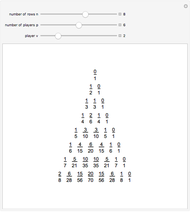
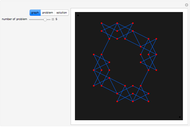
In this problem every  person is eliminated. By changing the number
person is eliminated. By changing the number  you can make an interesting animation.
you can make an interesting animation.
Permanent Citation