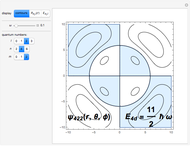
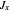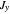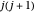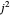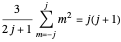Space-Quantization of Angular Momentum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The commutation relations for angular momentum in quantum mechanics are given by 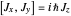 ,
, 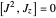 , with cyclic permutations. From these, the allowed values of quantized angular momentum can be derived, namely,
, with cyclic permutations. From these, the allowed values of quantized angular momentum can be derived, namely, 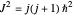 and
and  , with
, with 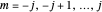 ,
, 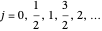 . Customarily, the
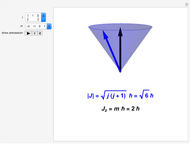
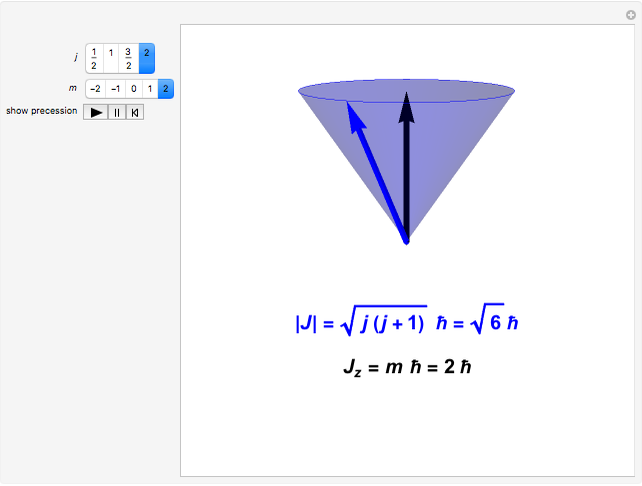
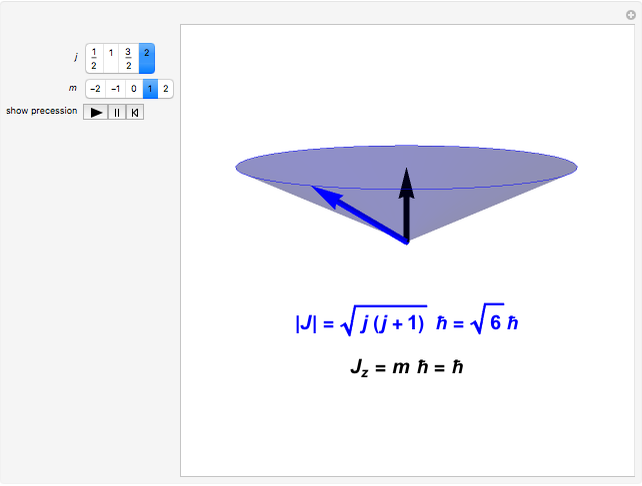
. Customarily, the  component is singled out, with the other two components retaining indefinite or fluctuating values (except when
component is singled out, with the other two components retaining indefinite or fluctuating values (except when  . The definite magnitude and direction of one component of angular momentum is known as "space quantization". Restriction of
. The definite magnitude and direction of one component of angular momentum is known as "space quantization". Restriction of 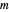 to integer values was exploited in Bohr's model of the hydrogen atom. When spin is involved,
to integer values was exploited in Bohr's model of the hydrogen atom. When spin is involved, 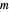 and
and 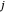 can also take half-integer values.
can also take half-integer values.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference: S. M. Blinder, Introduction to Quantum Mechanics, Amsterdam: Elsevier, 2004 pp. 83–85.
Permanent Citation