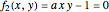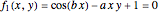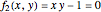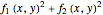Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

All Roots of Two Systems of Algebraic Equations

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

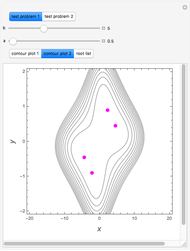
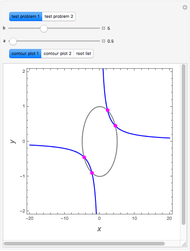
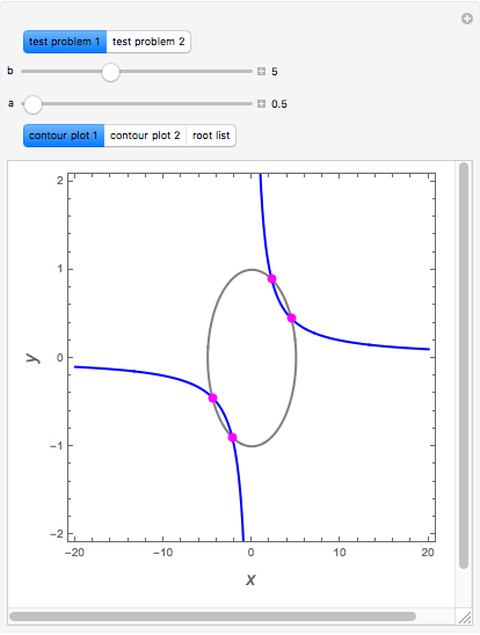
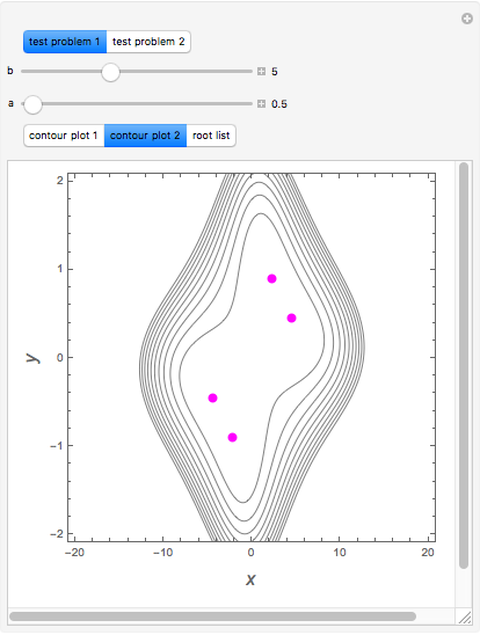
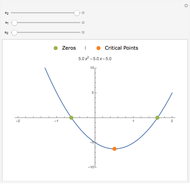
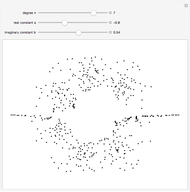
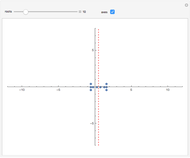
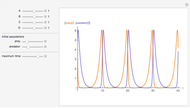
This Demonstration illustrates how one can use NDSolve's WhenEvent option to determine the roots of a system of nonlinear algebraic equations: 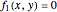and 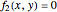. An attractive feature of the method is that one does not need not need to know at the outset an approximate guess for the roots. All one needs to do is specify the solution domain , .

[more]

Consider the two test problems consisting of two-dimensional systems of algebraic equations:

1. 
,

.

2. 
,

.

You can vary the parameters and .

This Demonstration finds all the roots of these two problems in the range (for test problem 1) and (for test problem 2).

The first contour plot is the graph of and , and the second shows the level curves of , which is minimized at a solution to the system.

[less]

Contributed by: Housam Binous, Ahmed Bellagi, and Brian G. Higgins (October 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The following describes the solution methodology.

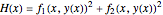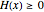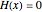First, define . By construction . If is a root of the system , then and 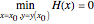. Thus, a necessary condition is given by .

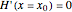You can solve the differential-algebraic system of equations:

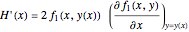Eq. (1),

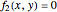Eq. (2).

In doing so, we are solving the ODE given by Eq. (1) along the curve 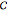defined in the x-y plane by Eq. (2). A solution to such a problem is always guaranteed for the particular case when the DAE system has index 1, which is equivalent to . We use the built-in Mathematica function WhenEvent to obtain the values of (i.e., the candidate roots) that verify the necessary condition 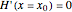. For each value of , we check if the system of equations is indeed verified by calculating . If , that particular candidate solution is simply rejected.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send