Angular Spheroidal Functions as a Function of Spheroidicity

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
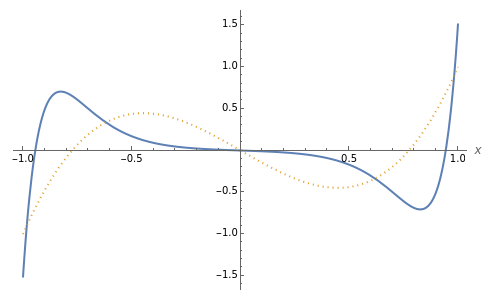
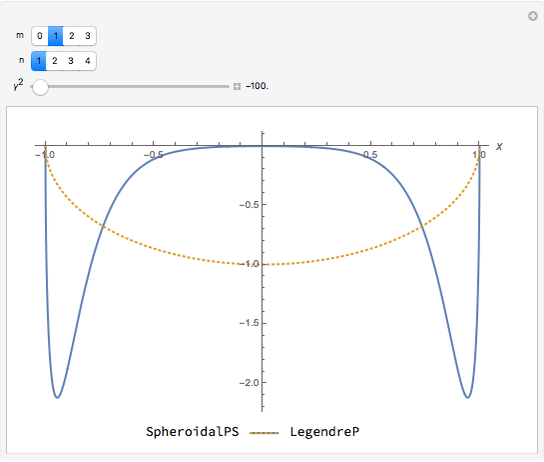
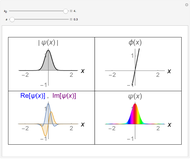
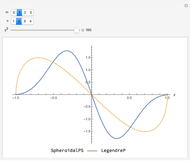
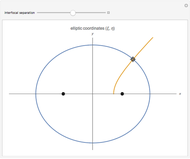
This Demonstration shows how the angular spheroidal functions,  , vary over the interval
, vary over the interval  . For comparison we also show the corresponding Legendre functions,
. For comparison we also show the corresponding Legendre functions,  , to which the spheroidal ones reduce when
, to which the spheroidal ones reduce when  . The controls allow
. The controls allow  to be varied: for
to be varied: for  (real
(real  ) we have the so-called prolate functions, while for
) we have the so-called prolate functions, while for  (imaginary
(imaginary  ) we have the oblate functions.
) we have the oblate functions.
Contributed by: Peter Falloon (November 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
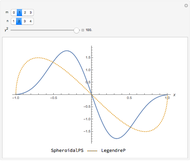
Snapshot 1: in the prolate limit  (where the spheroid becomes an infinite cylinder), the angular spheroidal functions become more concentrated around the origin (
(where the spheroid becomes an infinite cylinder), the angular spheroidal functions become more concentrated around the origin ( ), and less concentrated around the edges (
), and less concentrated around the edges ( )
)
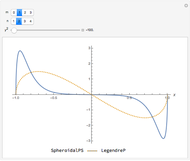
Snapshot 2: the reverse holds in the oblate limit  , in which the spheroid becomes a flat disk
, in which the spheroid becomes a flat disk
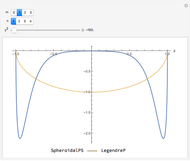
Snapshot 3: in the oblate limit, both even and odd functions vanish at  ; the even functions tend to the same form as the next higher odd function, with a sign change on one half of the interval (compare this picture, for
; the even functions tend to the same form as the next higher odd function, with a sign change on one half of the interval (compare this picture, for  , with Snapshot 2, where
, with Snapshot 2, where  )
)
Permanent Citation