Chooser Options

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
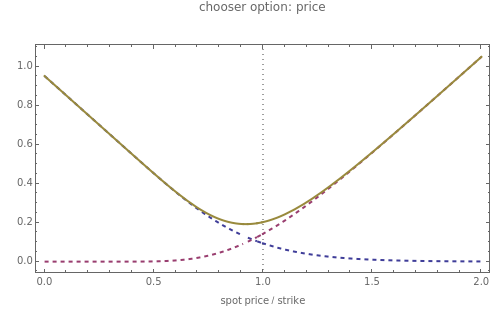
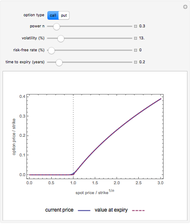
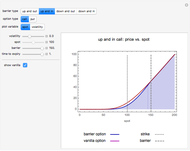
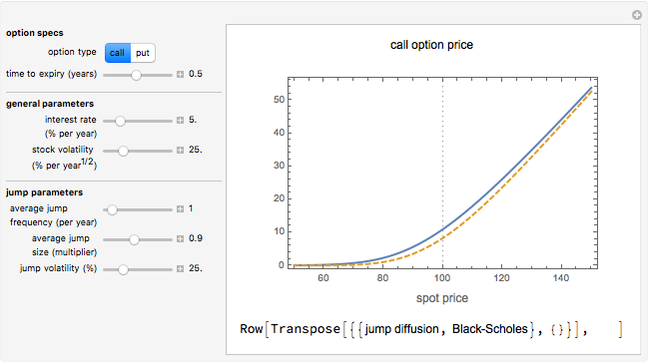
This Demonstration illustrates the price and "greeks" for chooser options in comparison to those for regular put and call options.
Contributed by: Peter Falloon (December 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Chooser options are a type of exotic option that, at some pre-specified time 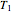 in the future, can be converted into either a put or call option with expiry
in the future, can be converted into either a put or call option with expiry 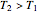 and strike
and strike 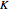 . The price of a chooser option,
. The price of a chooser option, 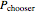 , thus tends to be higher than that of the corresponding call or put,
, thus tends to be higher than that of the corresponding call or put, 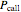 or
or 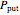 . The amount of extra value depends on
. The amount of extra value depends on 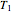 and
and 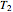 : for
: for 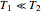 ,
, 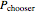 is approximately
is approximately 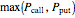 . As
. As 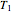 tends to
tends to 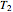 ,
, 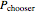 tends to
tends to 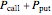 .
.
It can be shown using general put-call parity considerations that, for 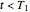 , a chooser option is equivalent to a portfolio comprising a call option with strike
, a chooser option is equivalent to a portfolio comprising a call option with strike 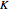 and expiry
and expiry 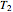 together with a put option with strike
together with a put option with strike 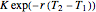 and expiry
and expiry 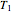 (assuming a constant interest rate
(assuming a constant interest rate  ). Within the Black–Scholes model, chooser options can therefore be priced using the solutions for call and put options.
). Within the Black–Scholes model, chooser options can therefore be priced using the solutions for call and put options.
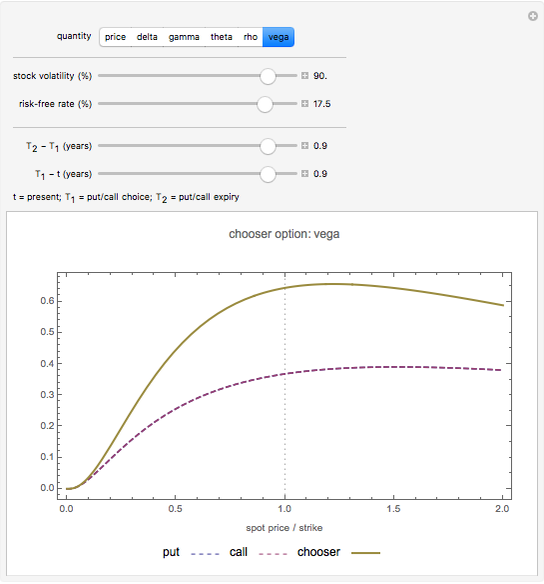
In this Demonstration, the price of chooser options is explored, as well as the derivative of the value function 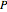 with respect to the various input parameters (the "greeks"): delta,
with respect to the various input parameters (the "greeks"): delta, 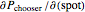 ; gamma,
; gamma, 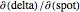 ; theta,
; theta, 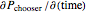 ; rho,
; rho, 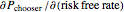 ; and vega,
; and vega, 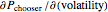 . For convenience, we assume zero dividends.
. For convenience, we assume zero dividends.
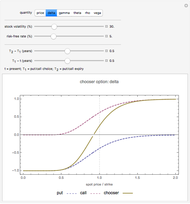
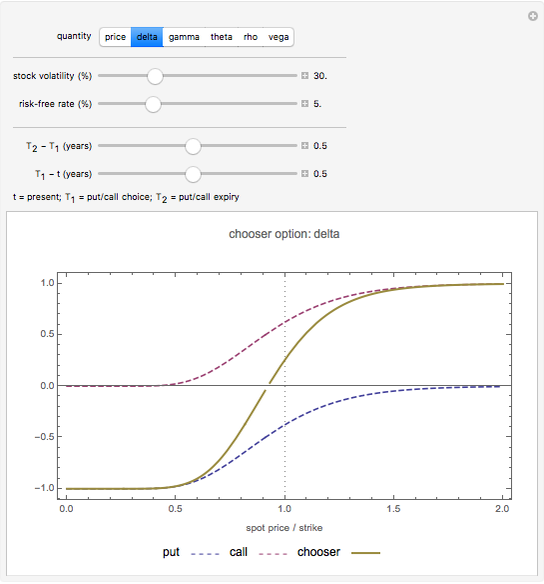
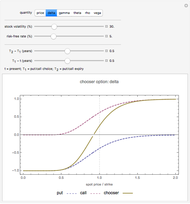
Snapshot 1: the "delta" of a chooser option can be either positive or negative, depending on whether the put or call is more valuable.
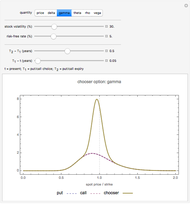
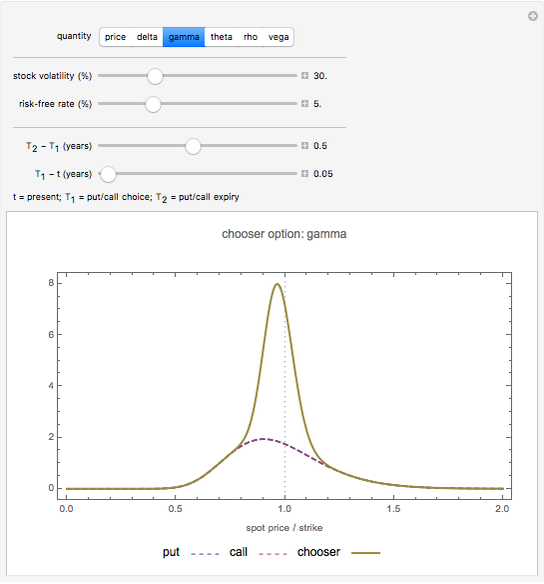
Snapshot 2: as  tends
tends 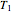 , the "gamma" of a chooser option becomes very large for a spot price close to the strike (i.e. "at the money"). This is because at
, the "gamma" of a chooser option becomes very large for a spot price close to the strike (i.e. "at the money"). This is because at 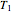 , the chooser option will become either a put or call option, which will have roughly opposite deltas at the money. Therefore, the delta of the chooser option will tend to change very quickly around
, the chooser option will become either a put or call option, which will have roughly opposite deltas at the money. Therefore, the delta of the chooser option will tend to change very quickly around 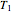 , and hence gamma is large.
, and hence gamma is large.
J. C. Hull, Options, Futures, and Other Derivatives, New Jersey: Prentice Hall, 2006.
E. G. Haug, The Complete Guide to Option Pricing Formulas, 2nd ed., New York: McGraw-Hill, 2007.
Permanent Citation