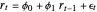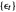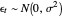Autocorrelation and Partial Autocorrelation Functions of AR(1) Process

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
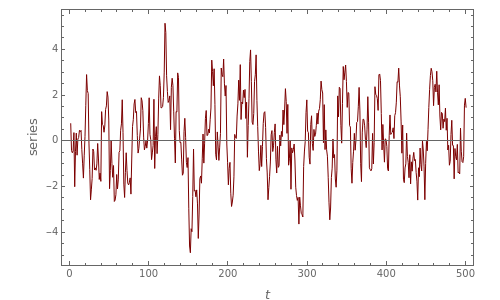
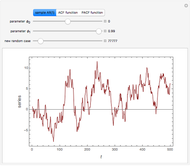
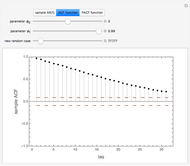
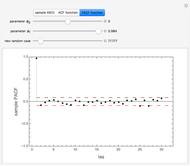
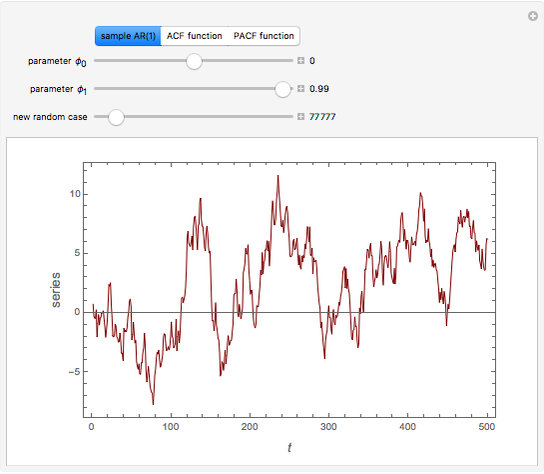
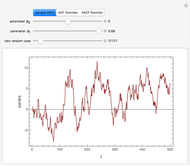
This Demonstration shows realizations of an autoregressive process of order one (AR(1)), its autocorrelation function (ACF), and its partial autocorrelation (PACF) function. The first tab, "sample AR(1)" shows realization of 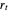 :
:
Contributed by: Jozef Barunik (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
An autoregressive process of order one can be described by:
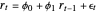 ,
,
where 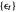 is assumed to be white noise with
is assumed to be white noise with 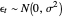 . A simple autoregressive model of order one (an AR(1) model) has the same form as a simple linear regression model, where
. A simple autoregressive model of order one (an AR(1) model) has the same form as a simple linear regression model, where 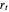 is dependent and
is dependent and 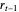 is the explanatory variable, but they have different properties. The mean and variance conditionals on past returns are:
is the explanatory variable, but they have different properties. The mean and variance conditionals on past returns are: 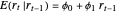 and
and 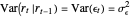 . Thus given the past return
. Thus given the past return 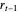 , the current return is centered around
, the current return is centered around 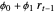 with variability
with variability 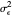 . Assuming that the series are weakly stationary,
. Assuming that the series are weakly stationary, 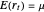 ,
, 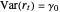 , and
, and 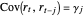 , where
, where  and
and 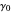 are constants. Necessary and sufficient conditions for the AR(1) model to be weakly stationary are
are constants. Necessary and sufficient conditions for the AR(1) model to be weakly stationary are  ; otherwise the process is explosive. The ACF of
; otherwise the process is explosive. The ACF of 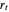 satisfies
satisfies 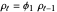 for
for 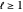 , but as
, but as 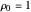 ,
, 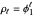 , and the ACF of a weakly stationary AR(1) series decays exponentially with rate
, and the ACF of a weakly stationary AR(1) series decays exponentially with rate 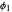 .
.
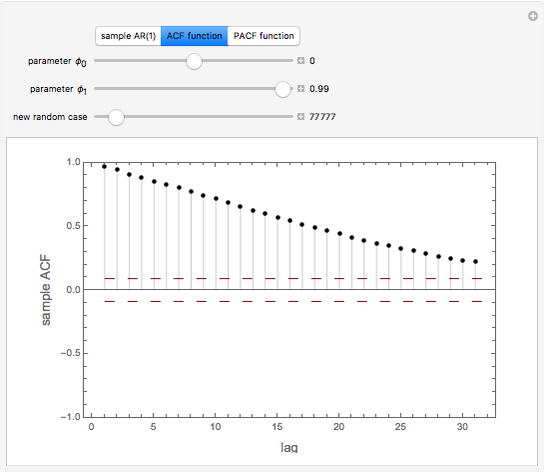
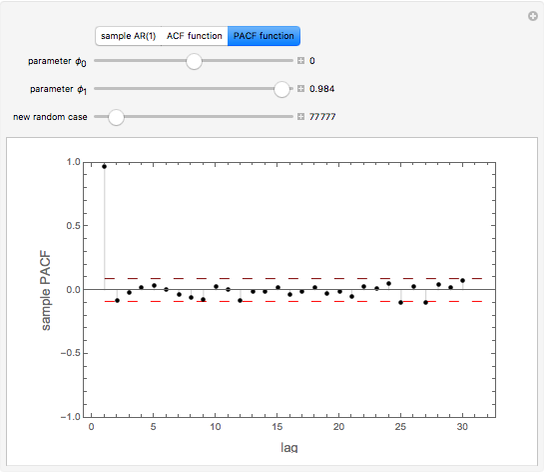
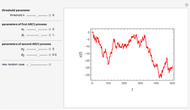
ACF and PACF are powerful tools for time series analysis. Snapshots 1, 2, and 3 show processes that are dependent (the parameter 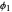 is large); you can observe slowly decaying strongly significant ACFs, while the PACF shows only one lag strongly significant. On the other hand, snapshots 4, 5, and 6 show a negatively dependent process, where the ACF is decaying exponentially and the PACF has again only one significant lag. Note that the significant lag of the PACF points to the AR(1) dependence in the observed time series, while the sign of the PACF lag corresponds to the sign of
is large); you can observe slowly decaying strongly significant ACFs, while the PACF shows only one lag strongly significant. On the other hand, snapshots 4, 5, and 6 show a negatively dependent process, where the ACF is decaying exponentially and the PACF has again only one significant lag. Note that the significant lag of the PACF points to the AR(1) dependence in the observed time series, while the sign of the PACF lag corresponds to the sign of 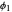 .
.
References:
J. D. Hamilton, Time Series Analysis, Princeton: Princeton University Press, 1994.
R. S. Tsay, Analysis of Financial Time Series, New York: Wiley, 2002.
Permanent Citation