Aliasing in Time Series Analysis
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
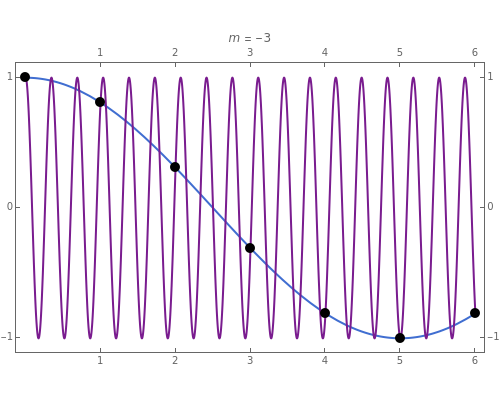
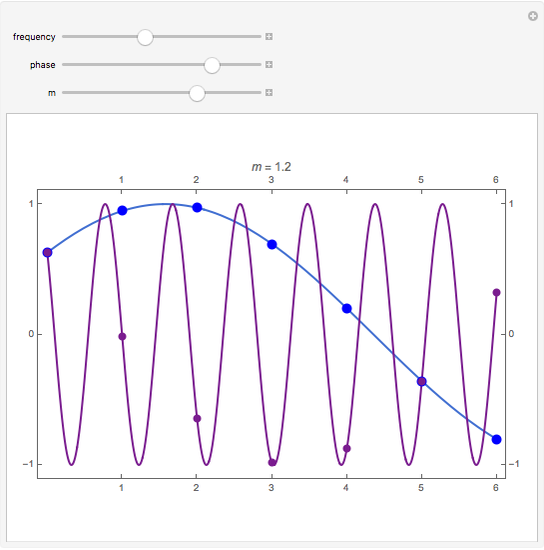
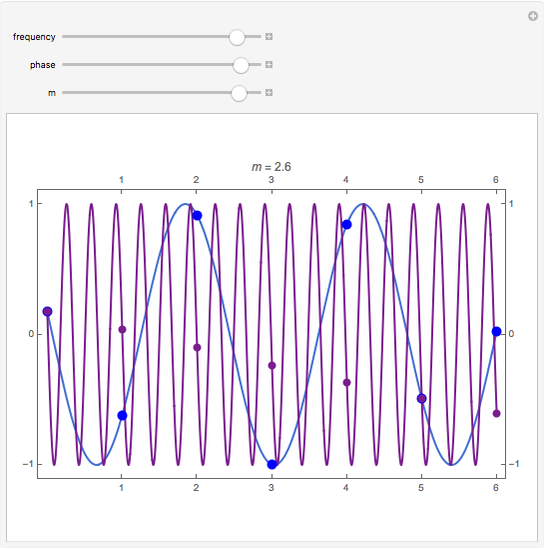
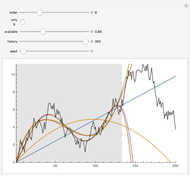
The relationship between two sinusoidal signals 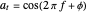 and
and 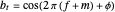 is shown for
is shown for 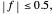
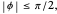 and
and 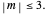 The signals are assumed to be observed at times
The signals are assumed to be observed at times 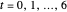 and the observed points are indicated. When
and the observed points are indicated. When  is an integer the points on the curve coincide and the signals are said to be aliased. Considering all frequencies in the range
is an integer the points on the curve coincide and the signals are said to be aliased. Considering all frequencies in the range 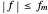 , the largest value of
, the largest value of 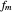 so that all signals may be identified from the observed points is called the Nyquist frequency. It is well known that
so that all signals may be identified from the observed points is called the Nyquist frequency. It is well known that 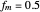 .
.
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
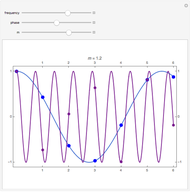
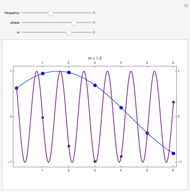
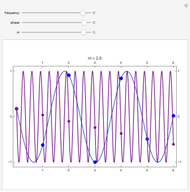
Snapshots
Details
$FailedPermanent Citation