Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Benford's Law in Statistical Physics

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

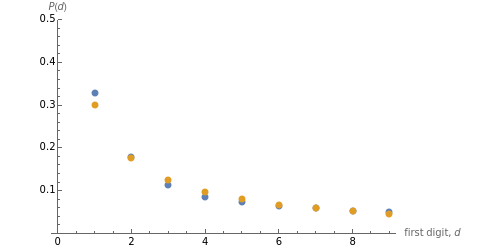
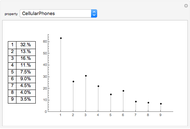
Benford's law is the observation that for many datasets, the distribution of their first significant digit follows a non-uniform law; the probability that is the leading digit is .

[more]

The Boltzmann–Gibbs (BG) and the Fermi–Dirac (FD) distributions are two frequently occurring statistical laws. This Demonstration shows that BG and FD distributions both fluctuate slightly in a periodic manner around the Benford distribution with the temperature of the system. The red points in the figure present Benford's law, while the blue ones present the first digit distributions of BG (or FD) statistics.

[less]

Contributed by: Da Pan, Lijing Shao, and Bo-Qiang Ma (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

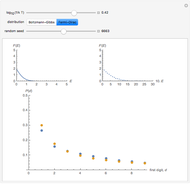
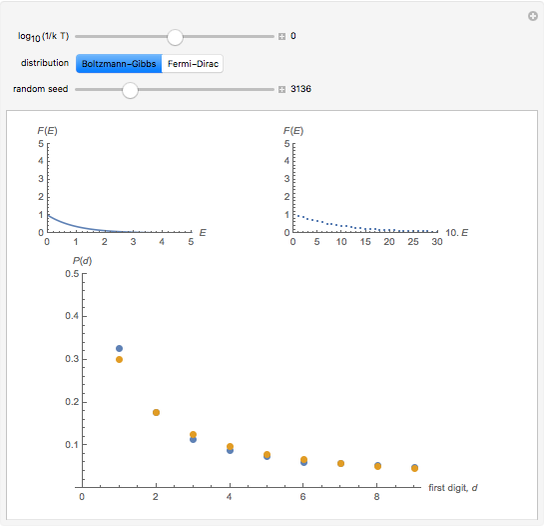
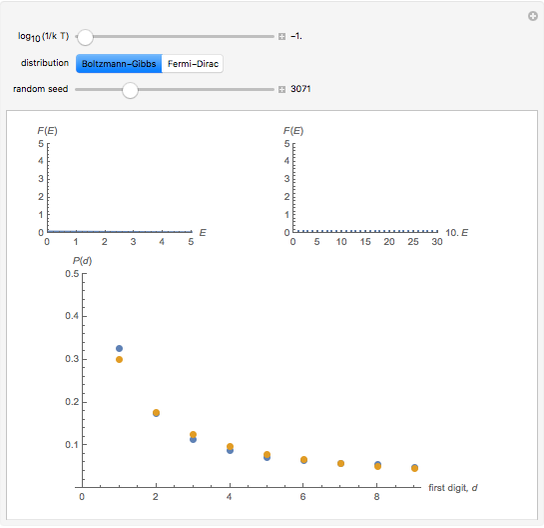
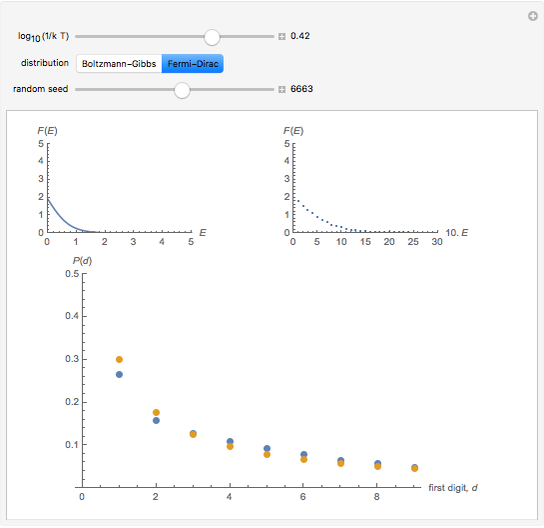
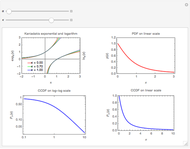
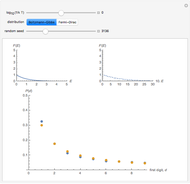
In this Demonstration, the first control is , where is the Boltzmann constant and is the system's temperature. This Demonstration shows clearly that for both distributions, the distribution of the first digit conforms approximately to Benford’s law with only slight fluctuations. By changing , you will find that the blue points oscillate periodically around the stationary red points. Another statistical law, the Bose–Einstein (BE) distribution, conforms to Benford's law exactly at all temperatures and therefore is not included here.

References

[1] S. Newcomb, "Note on the Frequency of the Use of Digits in Natural Numbers," American Journal of Mathematics, 4, 1881 pp. 39–40.

[2] F. Benford, "The Law of Anomalous Numbers," Proceedings of the American Philosophical Society 78(4), 1938 pp. 551–572.

[3] L. Shao and B-Q. Ma, "The Significant Digit Law in Statistical Physics," Physica A 389, 2010 pp. 3109–3116.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send