Benford's Law and Data Spread

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
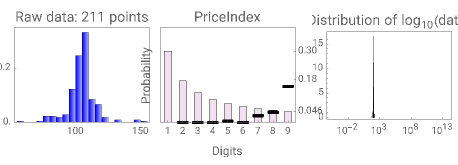
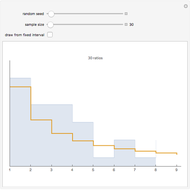
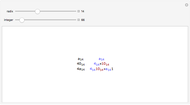
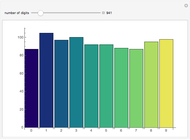
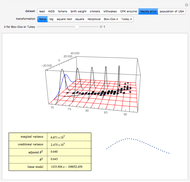
Benford's law is the observation that for many datasets, the distribution of their first significant digit follows a nonuniform law given by:
[more]
Contributed by: Stan Wagon (Macalester College) (March 2009)
Open content licensed under CC BY-NC-SA
Snapshots
Details
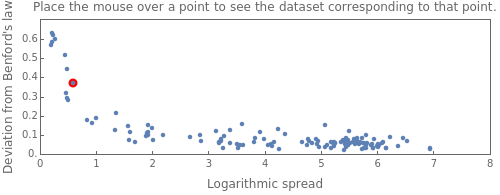
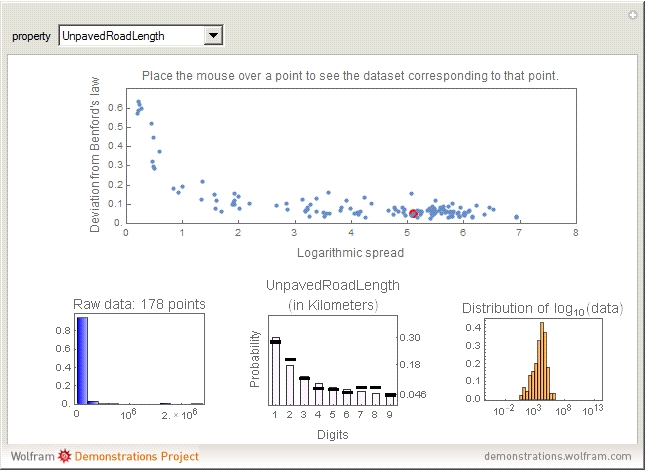
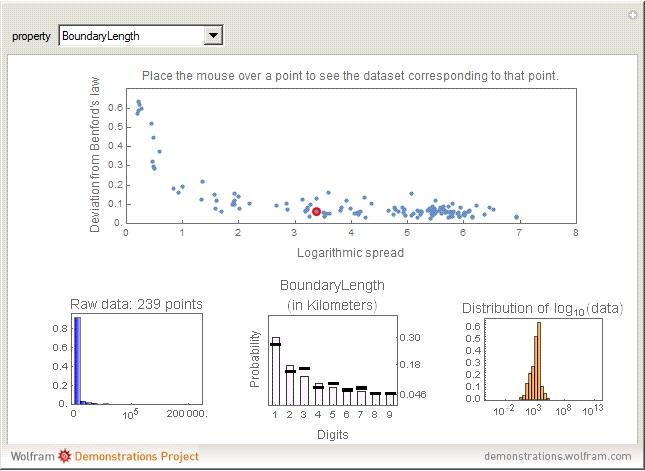
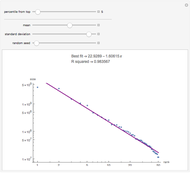
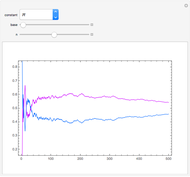
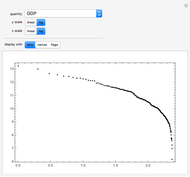
The connection between Benford's law and the spread of the data is lucidly described in [1] (see also Chapter 21 of [3] and Chapter 1 of [3]). The idea is that when viewing a distribution in a base-10 log scale, the proportion of the  axis corresponding to numbers beginning with 1 is
axis corresponding to numbers beginning with 1 is  . Hence, so long as there are several orders of magnitude, the error between this proportion and the proportion of the area lying above these numbers should be small.
. Hence, so long as there are several orders of magnitude, the error between this proportion and the proportion of the area lying above these numbers should be small.
[1] R. M. Fewster, "A Simple Explanation of Benford's Law," The American Statistician, 63(1), 2009 pp. 26-32.
[2] Benford's Law: Theory and Applications, edited by Steven J. Miller, Princeton: Princeton Univ. Pr., 2015.
[3] S. Wagon, Mathematica in Action, 3rd ed., New York: Springer, 2010.
Permanent Citation