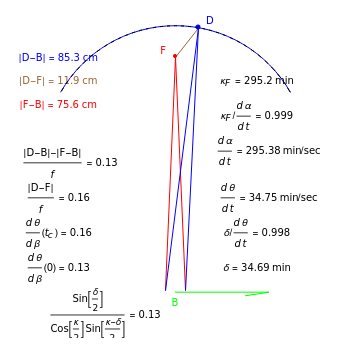
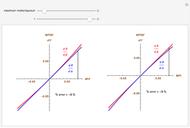
Dynamic Approximation of Static Quantities (Visual Depth Perception 14)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
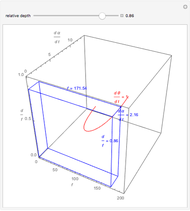
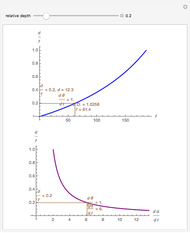
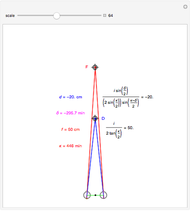
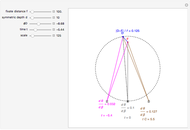
This Demonstration shows the asymptotic relation between  and
and  (binocular disparity) and between
(binocular disparity) and between 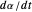 and
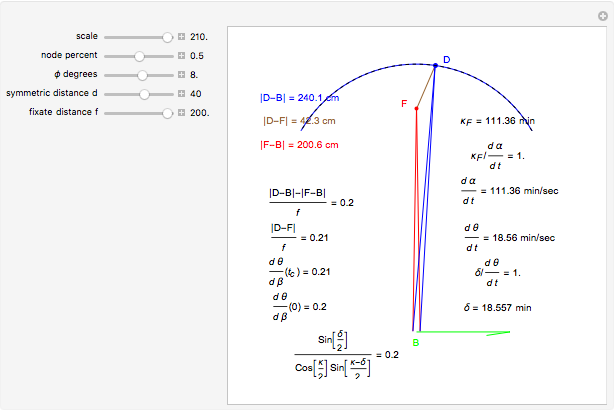
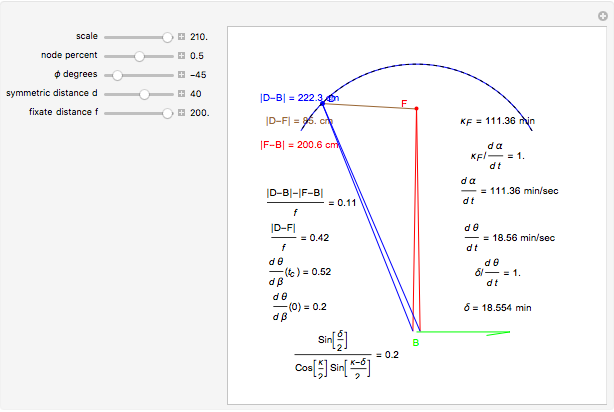
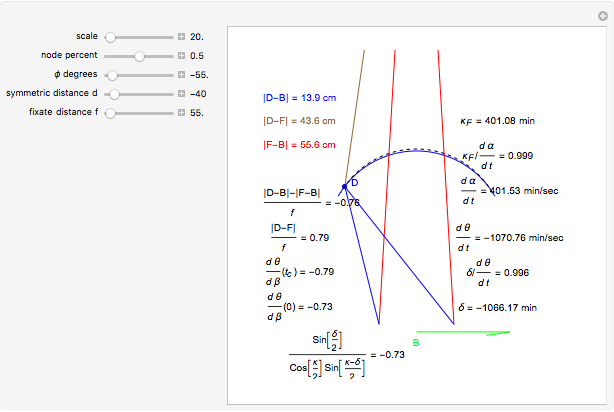
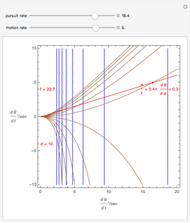
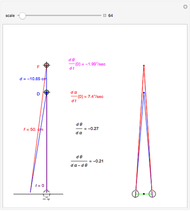
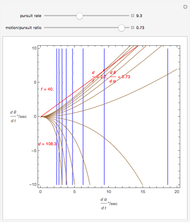
and 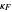 (fixate convergence angle). It also shows the motion/pursuit law at the critical time
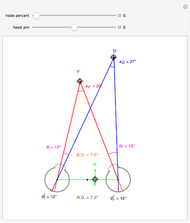
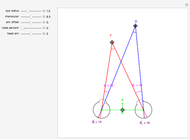
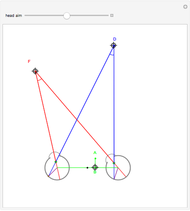
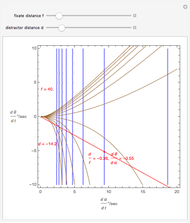
(fixate convergence angle). It also shows the motion/pursuit law at the critical time 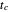 where it is a better two-dimensional measure of depth than the time zero M/PL or the static formula (based on the symmetric case). The angle slider moves the distractor around a circle where retinal motion is constant. The "node percent"
where it is a better two-dimensional measure of depth than the time zero M/PL or the static formula (based on the symmetric case). The angle slider moves the distractor around a circle where retinal motion is constant. The "node percent"  is the fraction of the eye radius where the node point lies with
is the fraction of the eye radius where the node point lies with 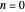 at the center of the eye.
at the center of the eye.
Contributed by: Keith Stroyan (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For translation perpendicular to the line of sight at 6.5 cm/sec (interocular distance per unit time), retinal motion, the derivative of  at
at 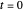 , approximates binocular disparity provided the fixate is far from the eyes and the distraction is not near the eyes. (Specifically, they are asymptotic (retinal motion/binocular disparity ≈1) provided the distractor is not more than 45° nasal angle and you are not near the Vieth–Müller circle.) If the speed is changed by a factor
, approximates binocular disparity provided the fixate is far from the eyes and the distraction is not near the eyes. (Specifically, they are asymptotic (retinal motion/binocular disparity ≈1) provided the distractor is not more than 45° nasal angle and you are not near the Vieth–Müller circle.) If the speed is changed by a factor  , then
, then 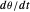 is also multiplied by
is also multiplied by  , so
, so
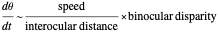 , when
, when  (the approximation is good as a percentage of
(the approximation is good as a percentage of  = B.D.).
= B.D.).
The multiplier effect means that at high speed, the  derivative is much larger than binocular disparity, so it can be detected more easily, even though, by itself, it is not sufficient to measure depth. (The rate of change
derivative is much larger than binocular disparity, so it can be detected more easily, even though, by itself, it is not sufficient to measure depth. (The rate of change 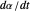 would also be magnified, but
would also be magnified, but 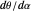 and the motion/pursuit formula would be unchanged.) This means people can detect depth from motion when they cannot detect the depth of the same objects when at rest. For example, the retinal disparity of an object 20 m beyond a fixate at 100 m is
and the motion/pursuit formula would be unchanged.) This means people can detect depth from motion when they cannot detect the depth of the same objects when at rest. For example, the retinal disparity of an object 20 m beyond a fixate at 100 m is 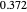 min of arc, below what people can detect, while at
min of arc, below what people can detect, while at 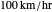 ,
,  = 159 min/sec.
= 159 min/sec.
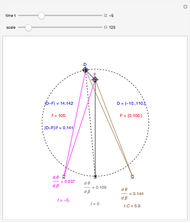
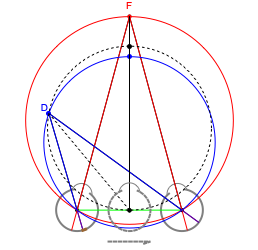
The retinal motion rate 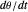 and motion/pursuit ratio
and motion/pursuit ratio 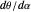 at
at 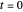 are constant on circles passing through the eye node and distractor
are constant on circles passing through the eye node and distractor 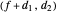 with diameter on the
with diameter on the 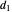 axis. (These circles are similar to the invariant circles for binocular disparity, but slightly different.)
axis. (These circles are similar to the invariant circles for binocular disparity, but slightly different.)
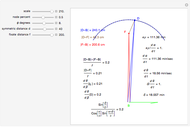
The pursuit rate satisfies 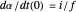 and the convergence of the eyes on the fixate satisfies
and the convergence of the eyes on the fixate satisfies 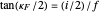 (when the eyes and fixate are symmetric). Sine and tangent are asymptotic to their argument for small angles,
(when the eyes and fixate are symmetric). Sine and tangent are asymptotic to their argument for small angles, 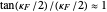 when
when 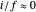 ; for large fixate distances we may replace sine or tangent with the angle (and cosine with 1).
; for large fixate distances we may replace sine or tangent with the angle (and cosine with 1).
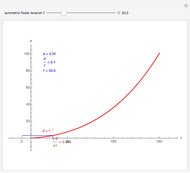
By simple geometry, the static relative depth for fixate and distractor on the 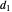 axis is
axis is
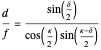 .
.
The two asymptotic relations above then show that the static relative depth formula is asymptotic to the motion/pursuit law (at 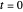 ):
):
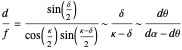 .
.
Permanent Citation