Classical Approximations of Pi

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
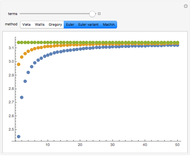
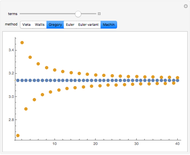
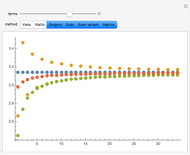
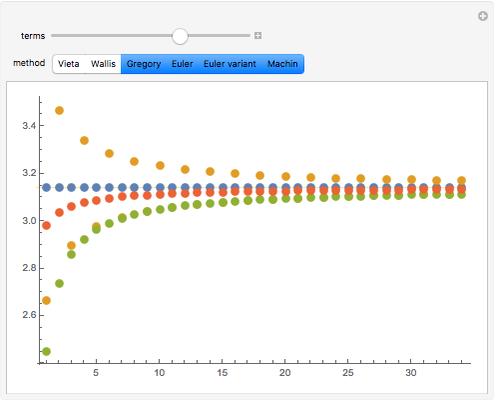
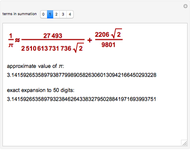
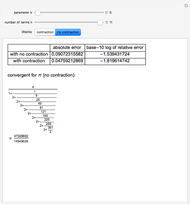
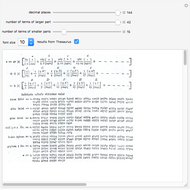
Since the discovery of  in antiquity, people have been fascinated with calculating its numerical value. Various infinite sums or products have been developed over the years. The success of such a method is determined by how fast it approaches its goal. This Demonstration compares several classical approximations for
in antiquity, people have been fascinated with calculating its numerical value. Various infinite sums or products have been developed over the years. The success of such a method is determined by how fast it approaches its goal. This Demonstration compares several classical approximations for  and their rates of convergence.
and their rates of convergence.
Contributed by: Rob Morris (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
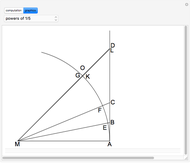
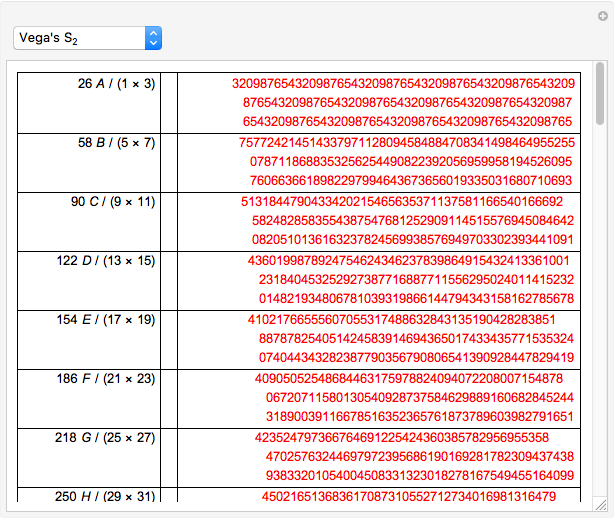
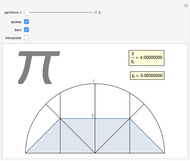
Here are the various methods used in this Demonstration:
Vieta's formula:
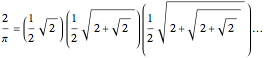
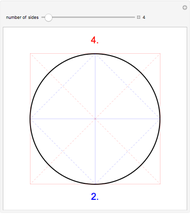
Wallis's product:
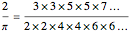
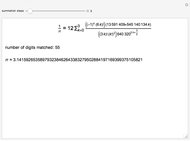
Gregory series:

Euler's series:
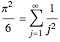
Euler's series variant:

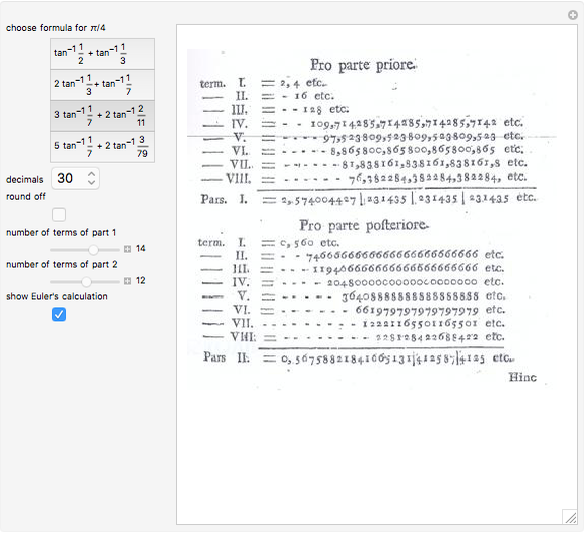
Machin's arc tangent formula:
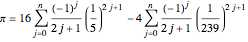
Permanent Citation