Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Comparing Algorithms for the Traveling Salesman Problem

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

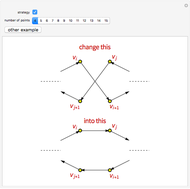
The traveling salesman problem (TSP) is an NP-complete problem. Different approximation algorithms have their advantages and disadvantages.

[more]

Mathematica's function FindShortestTour offers a choice of four methods ("OrZweig", "OrOpt", "TwoOpt", "CCA"), which may yield identical results.

This Demonstration provides another TSP algorithm called 3-Opt. Experiments show that the 3-Opt algorithm sometimes finds a better result than any of the four kinds of Mathematica FindShortestTour methods.

[less]

Contributed by: Frederick Wu (March 2011)
Additional contributions by: Daniel Lichtblau
Based on a program by: Sidong Zeng
Open content licensed under CC BY-NC-SA

Snapshots

Details

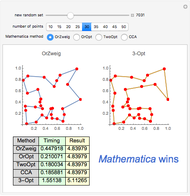
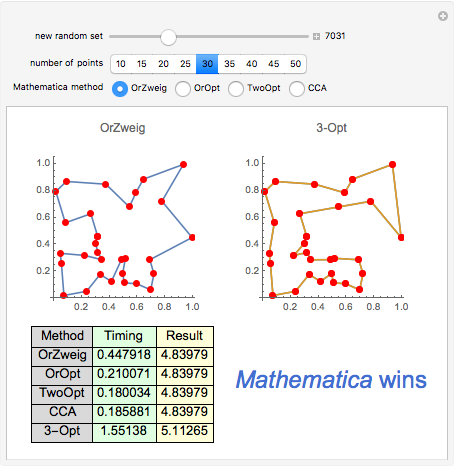
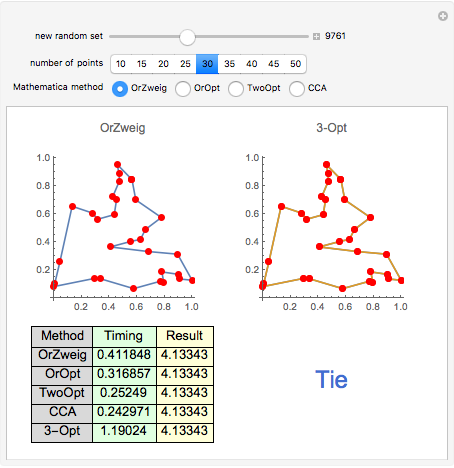
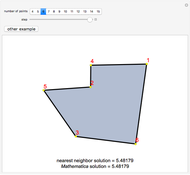
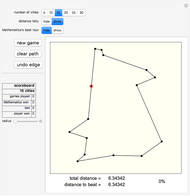
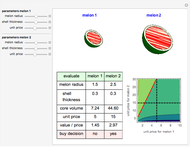
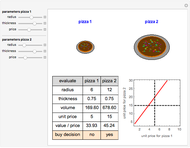
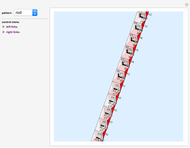
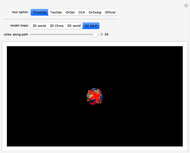
Snapshot 1: with 30 points, FindShortestTour methods find a shorter result than the 3-Opt method

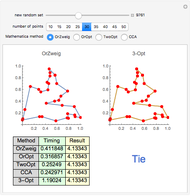
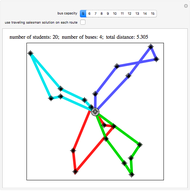
Snapshot 2: with 30 points, both 3-Opt and Mathematica's FindShortestTour methods find an optimal result

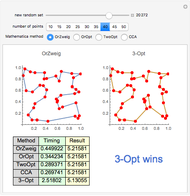
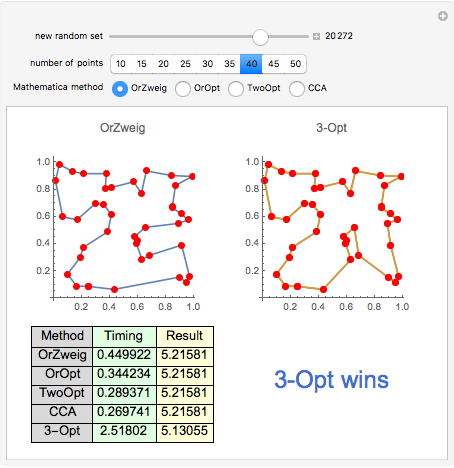
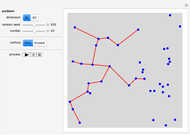
Snapshot 3: with 40 points, 3-Opt finds a shorter result than any of the FindShortestTour methods

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send