Traveling Salesman Game

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
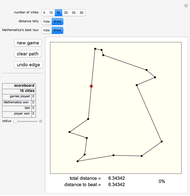
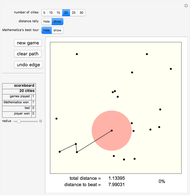
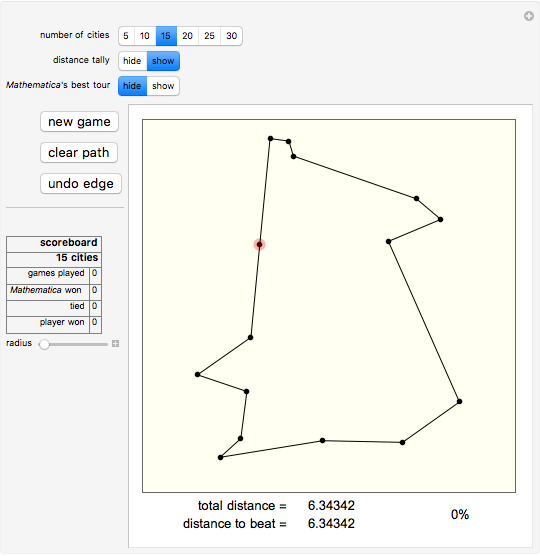
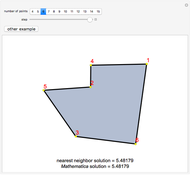
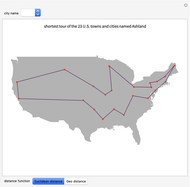
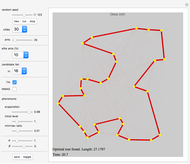
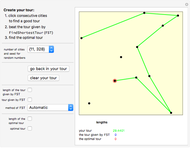
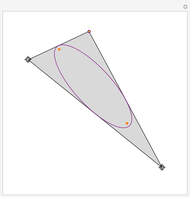
Attention gamers! You are a traveling salesman. Your task: visit the cities (represented as dots on the gameboard) one by one by clicking them. Start anywhere you like. You will trace out a route as you proceed. You must visit every city once and then return to your starting point. The goal is to find the shortest possible route that accomplishes this. Your total distance is recorded at the bottom of the panel, along with the total distance of the best route that Mathematica can find.
[more]
Contributed by: Bruce Torrence (March 2011)
Open content licensed under CC BY-NC-SA
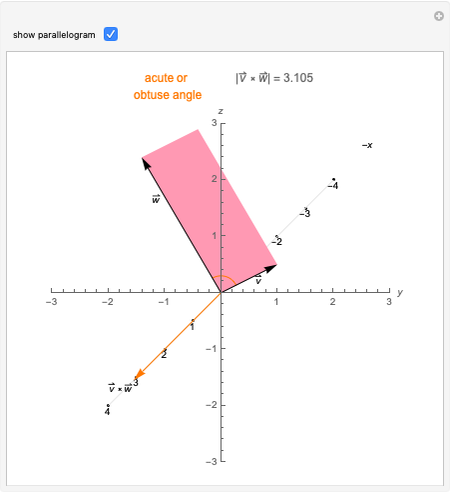
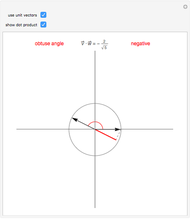
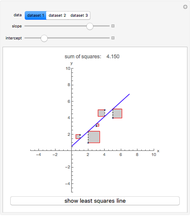
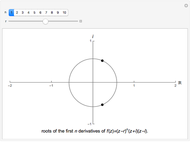
Snapshots
Details
The traveling salesman problem is a famous example of an NP-complete problem. There is no known algorithm that is guaranteed to solve every  -city problem in polynomial time (as a function of
-city problem in polynomial time (as a function of  ). Brute force is completely impractical. The total number of possible tours when there are
). Brute force is completely impractical. The total number of possible tours when there are  cities is
cities is  . So, for instance, with 30 cities there are 4420880996869850977271808000000 possible tours. Suffice it to say that calculating the length of each and then identifying the shortest among them is well beyond the capacity of today's computers. It is this reality that provides the possibility of "beating" Mathematica at this game.
. So, for instance, with 30 cities there are 4420880996869850977271808000000 possible tours. Suffice it to say that calculating the length of each and then identifying the shortest among them is well beyond the capacity of today's computers. It is this reality that provides the possibility of "beating" Mathematica at this game.
Mathematica uses the FindShortestTour command to find its best tour.
An excellent resource for all things TSP is William Cook's site, www.tsp.gatech.edu.
Permanent Citation