Variance-Bias Tradeoff

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
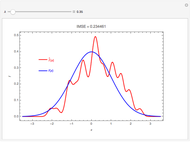
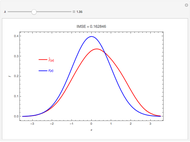
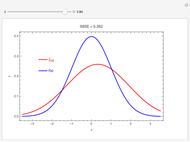
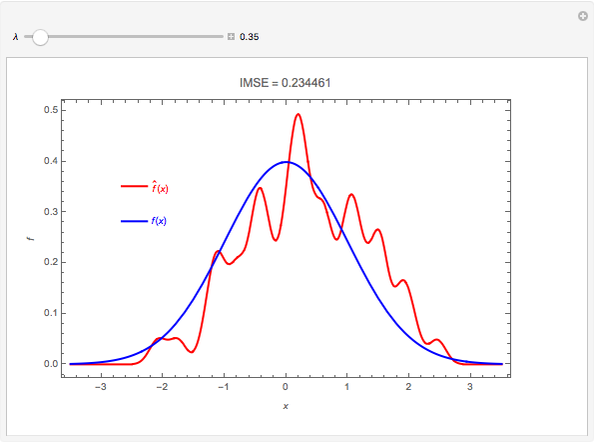
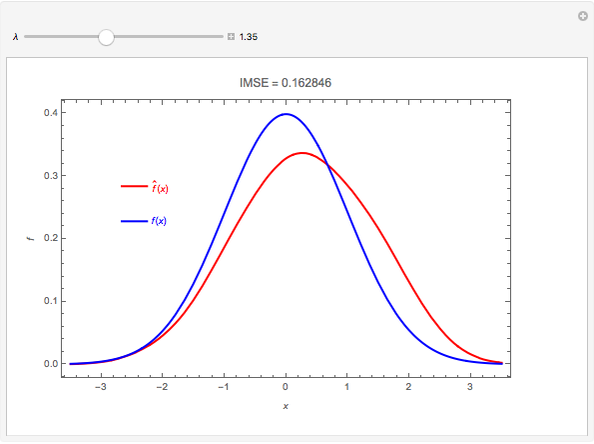
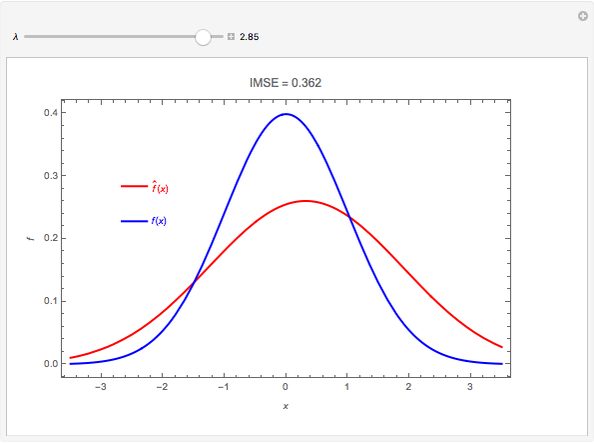
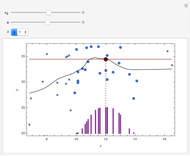
The plot shows the true density function  , which is normal with mean 0 and variance 1, and its nonparametric estimate
, which is normal with mean 0 and variance 1, and its nonparametric estimate  obtained using a kernel smoothing with parameter
obtained using a kernel smoothing with parameter  . The initial value for
. The initial value for  of 0.95 corresponds to the kernel smoother that minimizes the integrated mean-square error, IMSE. Graphically, IMSE is the area between the two curves. Smaller values correspond to less smoothing and larger to more smoothing. With less smoothing, the red curve wobbles more around the true value, but there is less systematic bias.
of 0.95 corresponds to the kernel smoother that minimizes the integrated mean-square error, IMSE. Graphically, IMSE is the area between the two curves. Smaller values correspond to less smoothing and larger to more smoothing. With less smoothing, the red curve wobbles more around the true value, but there is less systematic bias.
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The variance-bias tradeoff is most simply explained mathematically in terms of estimating a single parameter  with an estimator
with an estimator  . Then the mean-square error of estimation for
. Then the mean-square error of estimation for  provides an estimate of the accuracy of the estimator and is defined by
provides an estimate of the accuracy of the estimator and is defined by  ,
where
,
where  denotes mathematical expectation. The bias is defined by
denotes mathematical expectation. The bias is defined by  and the variance is
and the variance is  ; hence
; hence  . Thus there are two components to the error of estimation—one due to bias and the other variance.
. Thus there are two components to the error of estimation—one due to bias and the other variance.
This paradigm is very general and includes all statistical modelling problems involving smoothing or parameter estimation. For a more general discussion of this aspect, see §2.9 of T. Hastie, R. Tibshirani, and J. Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed., New York: Springer, 2009.
Permanent Citation