Compressible Flow through a Nozzle/Diffuser

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
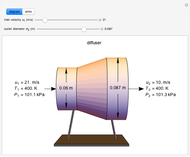
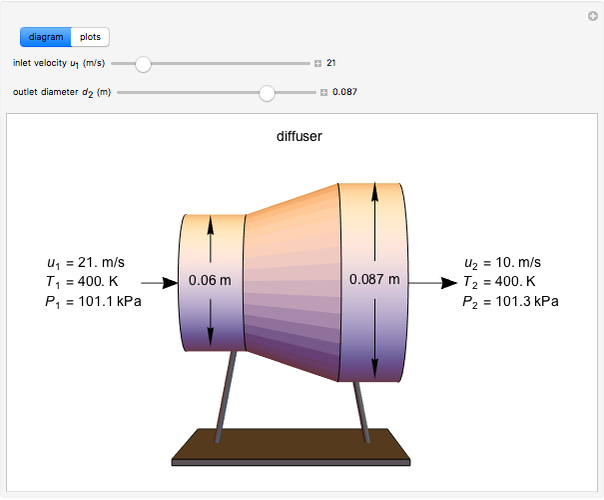
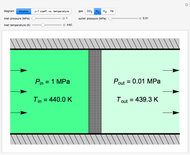
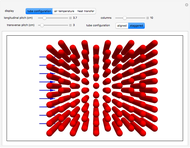
This Demonstration models compressible flow of air through a reversible nozzle/diffuser. The inlet pressure  , exit velocity
, exit velocity  , and exit temperature
, and exit temperature  are calculated from mass and energy balances. Because the system is reversible, the entropy change is zero. The air exits as a free jet at atmospheric pressure (
are calculated from mass and energy balances. Because the system is reversible, the entropy change is zero. The air exits as a free jet at atmospheric pressure ( ). Set the outlet diameter
). Set the outlet diameter  and inlet velocity
and inlet velocity  with sliders. When
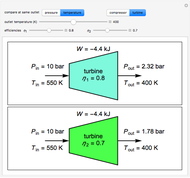
with sliders. When  , the device acts as a nozzle, with the inlet pressure higher than the exit pressure (
, the device acts as a nozzle, with the inlet pressure higher than the exit pressure ( ) in order to provide the energy needed to accelerate the air through the nozzle. When
) in order to provide the energy needed to accelerate the air through the nozzle. When  , the device operates as a diffuser, and the exit pressure is higher than the inlet pressure (
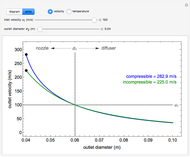
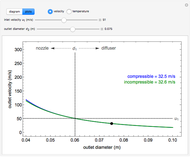
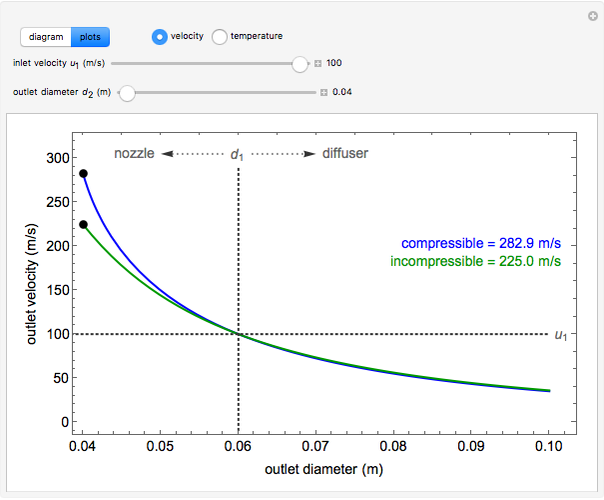
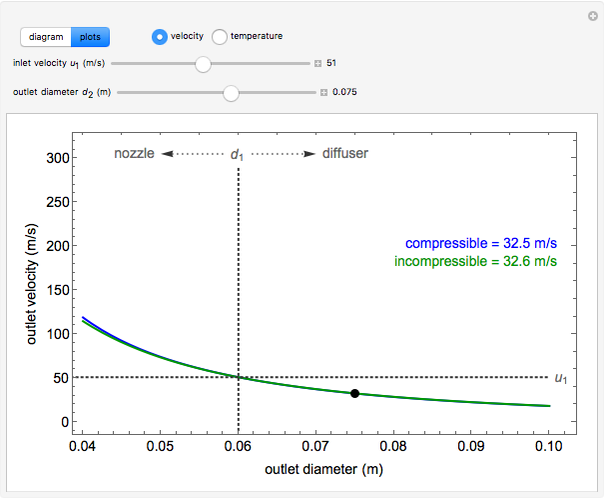
, the device operates as a diffuser, and the exit pressure is higher than the inlet pressure ( ). Select "plots" to plot the outlet velocity or outlet temperature as a function of outlet diameter for compressible air flow (blue) and incompressible air flow (green). Air is assumed to behave as an ideal gas and all flow is subsonic.
). Select "plots" to plot the outlet velocity or outlet temperature as a function of outlet diameter for compressible air flow (blue) and incompressible air flow (green). Air is assumed to behave as an ideal gas and all flow is subsonic.
Contributed by: Rachael L. Baumann (March 2016)
Additional contributions by: Jeffrey S. Knutsen andJohn L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The mass balance around a nozzle/diffuser for compressible flow where  for the inlet and
for the inlet and 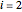 for the outlet is given by:
for the outlet is given by:
 ,
,
where  is the area,
is the area,  is the velocity (m/s),
is the velocity (m/s),  is the density calculated from the ideal gas law,
is the density calculated from the ideal gas law,  is diameter (m),
is diameter (m),  is pressure (kPa),
is pressure (kPa),  is the ideal gas constant and
is the ideal gas constant and  is temperature (K).
is temperature (K).
The mass balance simplifies to:

for incompressible flow  , and thus
, and thus  .
.
The energy balance for an adiabatic nozzle/diffuser is:
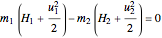 ,
,
where  is enthalpy (J/kg), and conservation of mass means that
is enthalpy (J/kg), and conservation of mass means that  , so the energy balance simplifies to:
, so the energy balance simplifies to:
 ,
,
where  is the ideal gas heat capacity of air (J/[kg K]).
is the ideal gas heat capacity of air (J/[kg K]).
For compressible flow, the inlet pressure  is calculated from an entropy balance on an adiabatic reversible system:
is calculated from an entropy balance on an adiabatic reversible system:
 ,
,
which simplifies to
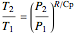 .
.
Permanent Citation