Parallel and Counterflow Heat Exchangers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
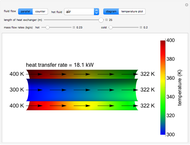
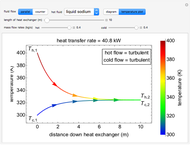
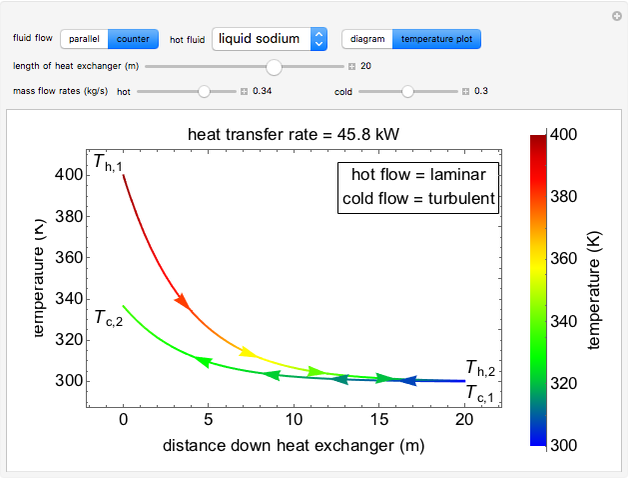
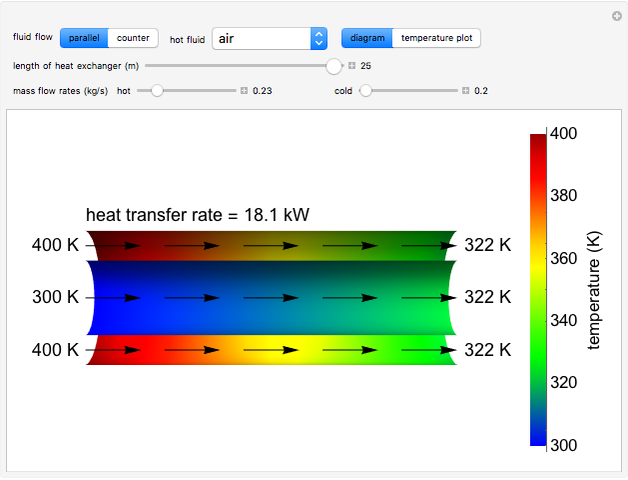
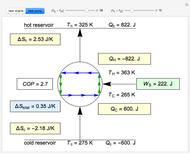
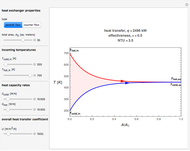
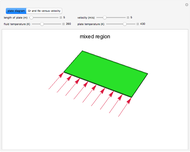
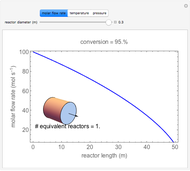
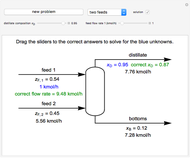
This Demonstration calculates temperatures and the rate of heat transfer in a concentric tube heat exchanger. The cold fluid is liquid water, which flows through the center of the heat exchanger. Select the hot fluid (air, liquid water, liquid sodium), which flows through the annular region, from the drop-down menu. Use buttons to select either parallel or counterflow. Set the length of the heat exchanger and the mass flow rates of the hot and cold fluids with sliders. Select "diagram" to show a schematic of the heat exchanger. Select "temperature plot" to show a plot of temperature versus distance through the heat exchanger for each stream. In both displays, colors represent the temperature (using the color scale on the right) and arrows indicate the direction of flow.
Contributed by: Rachael L. Baumann (May 2016)
Additional contributions by: John L. Falconer and Nathan S. Nelson
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The temperatures of the hot stream 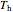 and the cold stream
and the cold stream 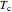 of the heat exchanger are calculated from these differential equations:
of the heat exchanger are calculated from these differential equations:
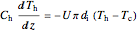 ,
,
for parallel flow:
 ,
,
for counterflow:
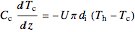 ,
,
where 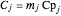 ,
, 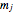 is mass flow rate (kg/s),
is mass flow rate (kg/s), 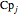 is heat capacity (J/[kg K]),
is heat capacity (J/[kg K]),  is length down the heat exchanger (m),
is length down the heat exchanger (m), 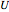 is the overall heat transfer coefficient (
is the overall heat transfer coefficient (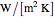 ) and
) and 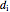 is the inner diameter (m).
is the inner diameter (m).
The overall heat transfer coefficient is calculated using the heat transfer coefficients of the cold 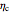 and hot
and hot 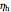 streams:
streams:
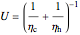 .
.
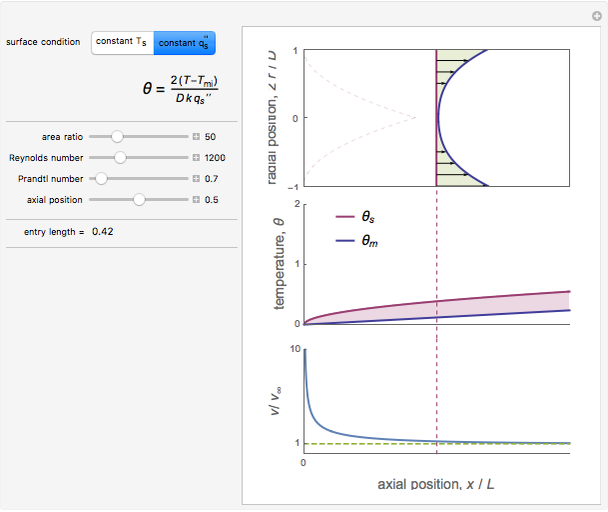
The heat transfer coefficients are calculated from Nusselt correlations. The Reynolds number is:
 ,
,
where 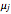 is the dynamic viscosity (
is the dynamic viscosity ( ),
), 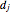 is the diameter (m) where
is the diameter (m) where 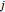 is
is  or
or 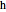 for the cold or hot streams. The diameter of the tube that the cold fluid flows through is
for the cold or hot streams. The diameter of the tube that the cold fluid flows through is  , and the hydraulic diameter of the annulus that the hot fluid flows through is
, and the hydraulic diameter of the annulus that the hot fluid flows through is 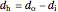 , where
, where 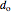 is the outer diameter.
is the outer diameter.
For turbulent flow (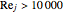 ), the Dittus–Boelter correlation for the Nusselt number is used:
), the Dittus–Boelter correlation for the Nusselt number is used:
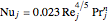 ;
;
otherwise,  is used for laminar flow,
is used for laminar flow,
where  is the Prandtl number,
is the Prandtl number, 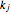 is thermal conductivity (W/[m K]),
is thermal conductivity (W/[m K]), 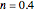 for heating and
for heating and 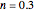 for cooling.
for cooling.
The heat transfer coefficients for each stream are calculated from 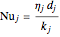 .
.
Reference
[1] T. L. Bergman, A. S. Lavine, F. P. Incropera and D. P. DeWitt, Introduction to Heat Transfer, 6th ed., Hoboken: John Wiley and Sons, 2011.
Permanent Citation