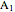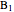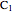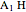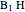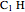Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Concurrent Lines that Intersect on the Euler Line

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

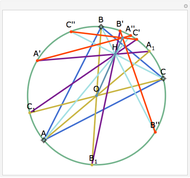
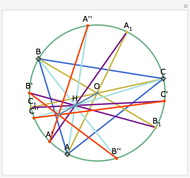
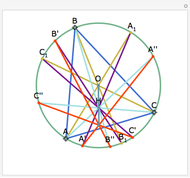
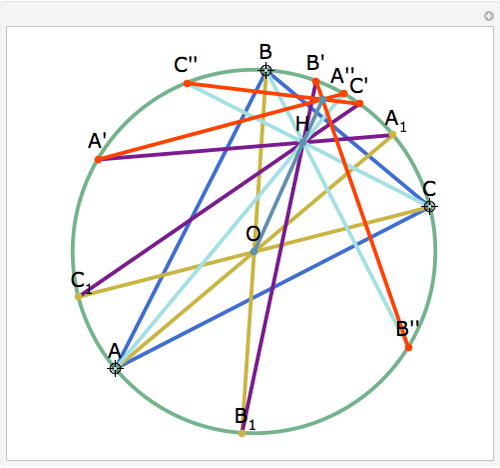
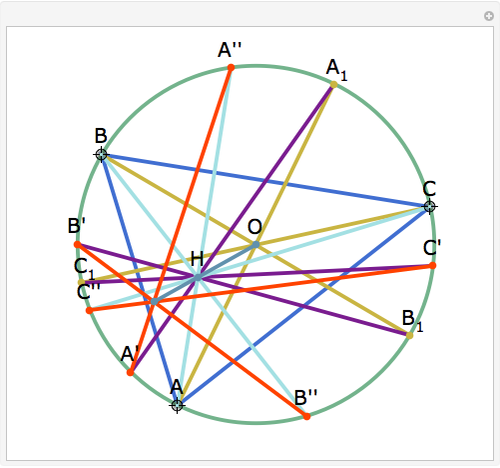
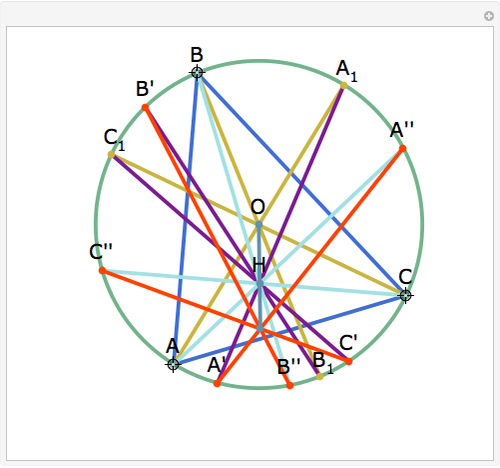
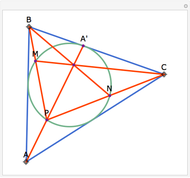
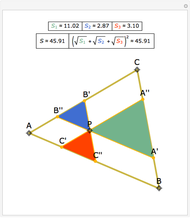
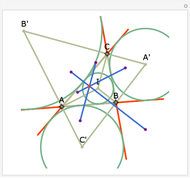
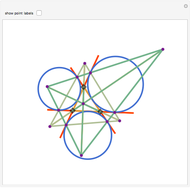
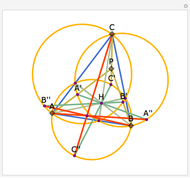
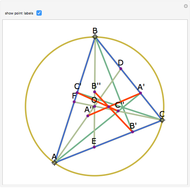
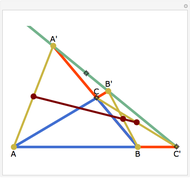
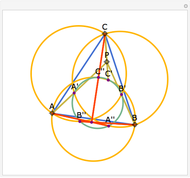
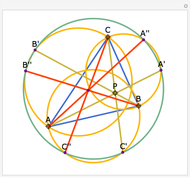
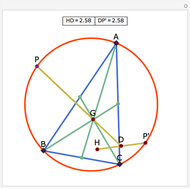
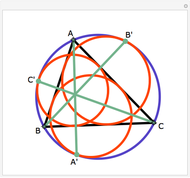
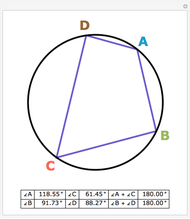
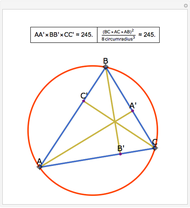
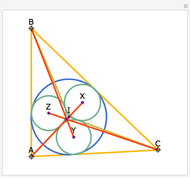
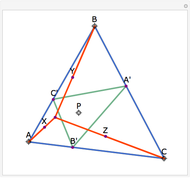
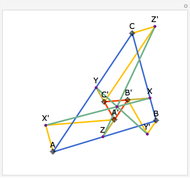
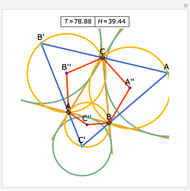
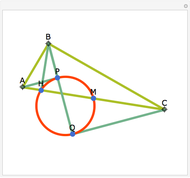
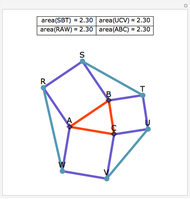
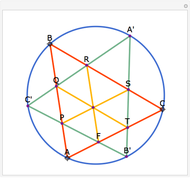
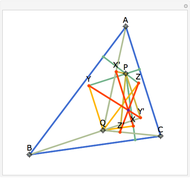
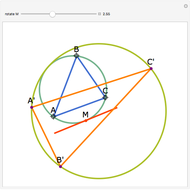
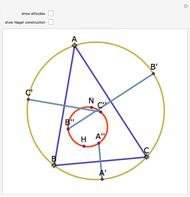
The Euler line of a triangle goes through the circumcenter and the orthocenter.

[more]

Let ABC be a triangle. Let O be the circumcenter and H the orthocenter of ABC. Let the intersection of AO, BO, and CO with the circumcircle be , , and , respectively. Let the intersection of , , and with the circumcircle be A', B', and C', respectively. Let the intersection of AH, BH, and CH with the circumcircle be A'', B'', and C'', respectively. Then A'A'', B'B'', and C'C'' are concurrent with the Euler line.

[less]

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

See problem 5 for day 2 in the Iranian 2005 National Math Olympiad (3rd round).

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send