,

,

where is the height of tank in meters, (set to 1 here) is the area of each tank in , is the inlet flow rate (the manipulated variable) into the first tank, and and are the outlet flow rates (expressed in ) from the first and second tank, respectively. The initial height of the liquid in each tank is assumed to be 0.25 meters.

The flow equation is given by where or and is the valve constant expressed in ). It is assumed that and .

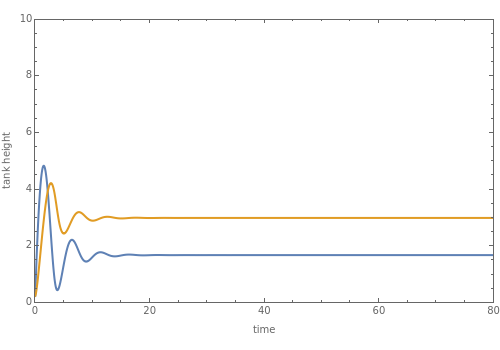
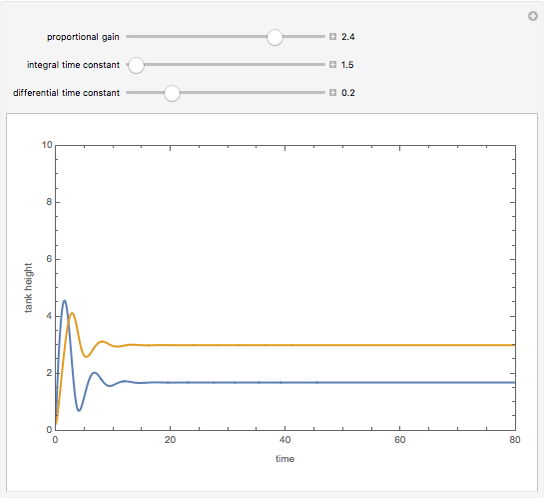
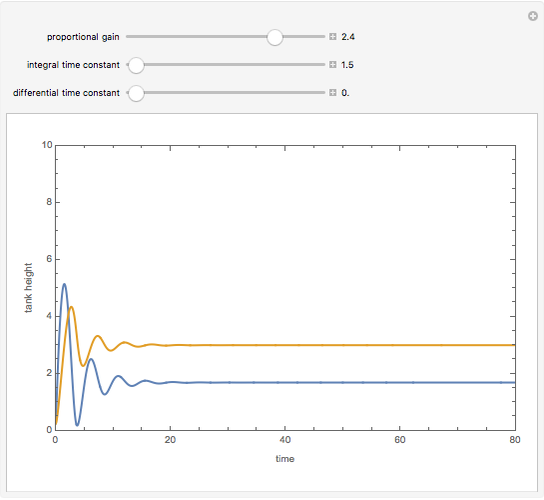
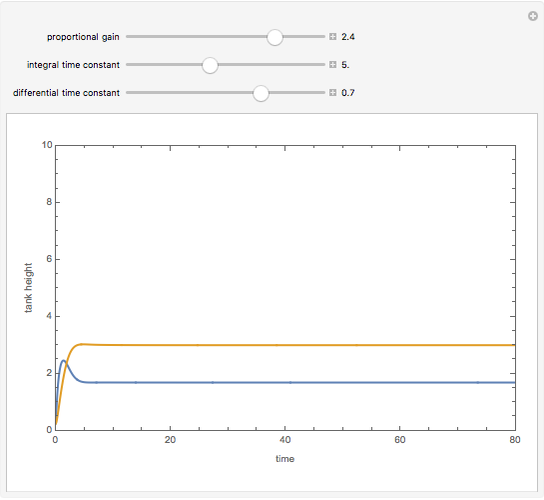
The setpoint for the height of the liquid (the process variable) in the second tank is chosen to be 3 meters.

The inlet flow rate is varied in order to achieve the desired setpoint value using P, PI, or PID (proportional–integral–derivative) control: , where is the error, is the proportional gain, and and are the integral and differential time constants, respectively.

For very large and , one recovers the usual proportional control, which is usually characterized by a small offset value (i.e., the final steady state height is not exactly equal to the setpoint value).

PI control is achieved when is taken equal to zero. PI control can show an overshoot and dumped oscillations around the setpoint. No offset is observed and the final steady state tank height is equal exactly to the setpoint value.

The most general case is when and is not too large; one gets PID control of the second tank's height.

The Demonstration plots the height of both tanks as a function of time; the blue curve displays and the magenta curve represents .