Cooling by a Cylindrical Pin Fin

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
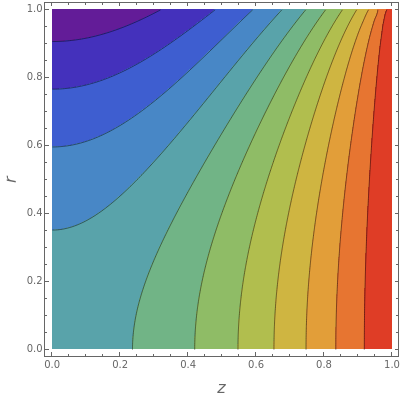
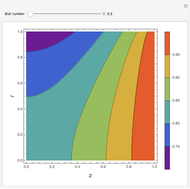
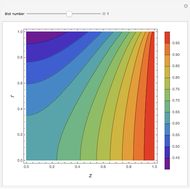
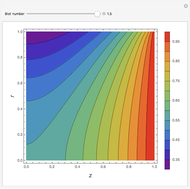
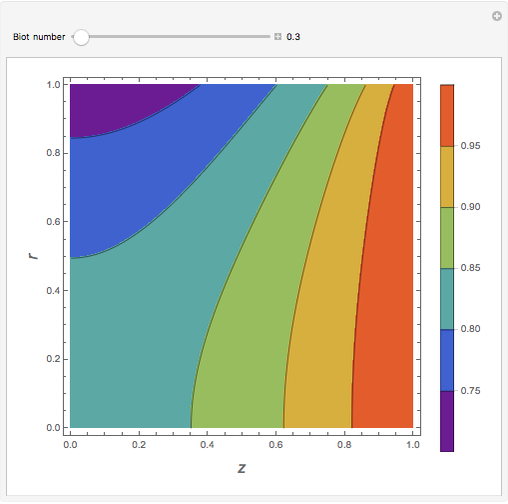
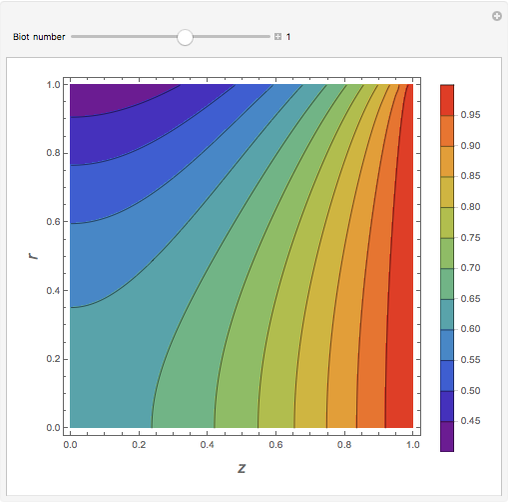
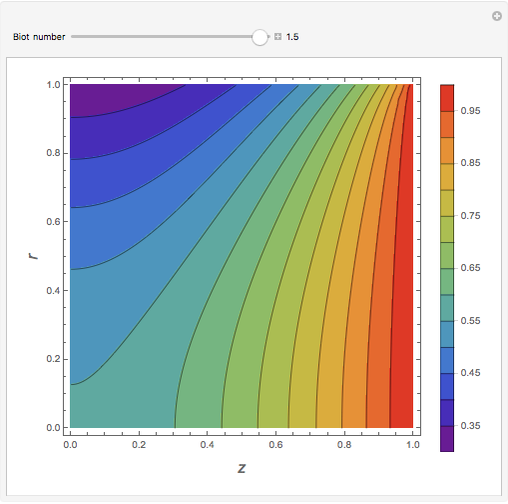
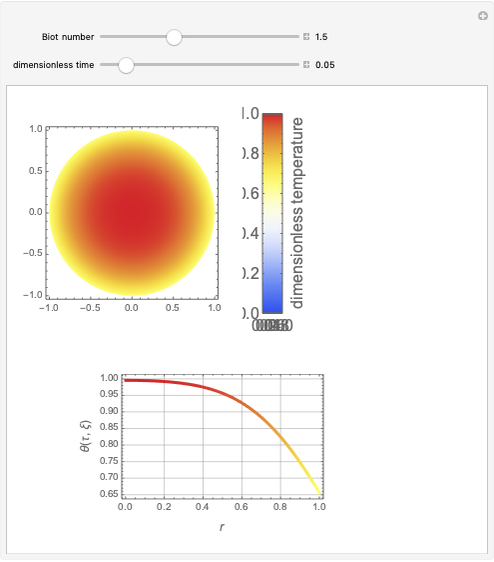
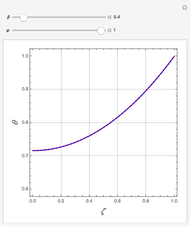
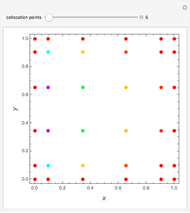
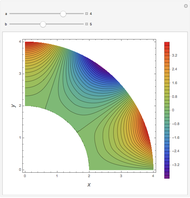
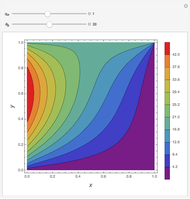
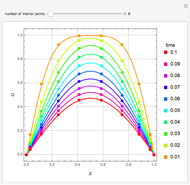
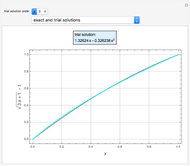
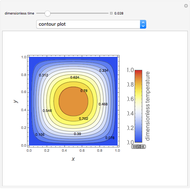
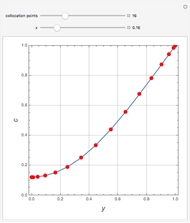
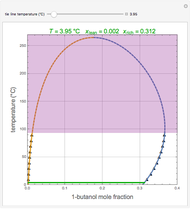
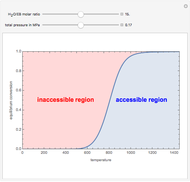
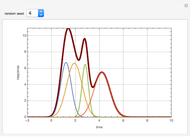
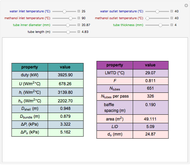
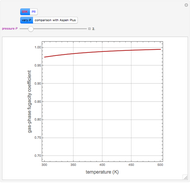
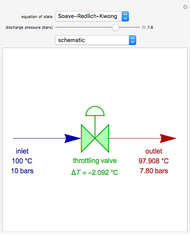
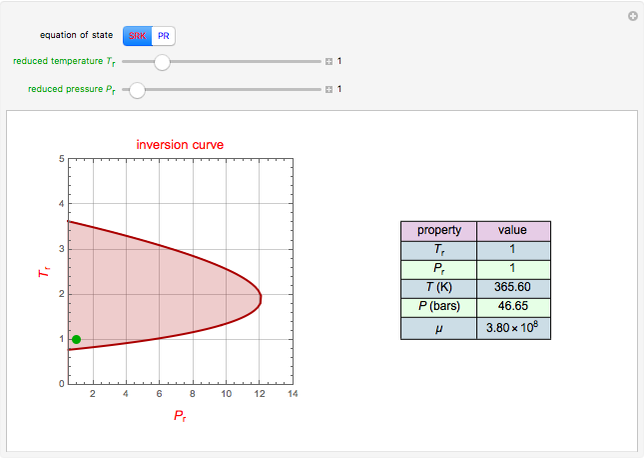
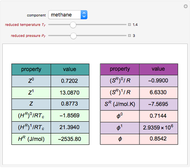
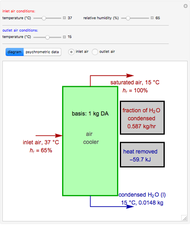
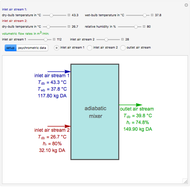
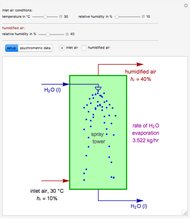
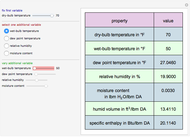
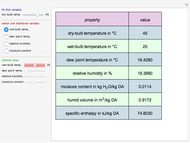
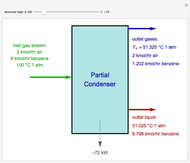
In electronic systems, a fin is a heat sink or a passive heat exchanger that cools a device by dissipating heat into the surrounding medium (e.g. air). This diagram shows a cylindrical pin fin, used to maximize heat transfer to a fluid between two walls:
[more]Contributed by: Housam Binous and Ahmed Bellagi (August 2015)
Snapshots
Details
Reference
[1] T. Bennett, Transport by Advection and Diffusion, New York: Wiley, 2012.
Permanent Citation
"Cooling by a Cylindrical Pin Fin
"
http://demonstrations.wolfram.com/CoolingByACylindricalPinFin/
Wolfram Demonstrations Project
Published: August 18 2015