Cycloidal Pendulum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
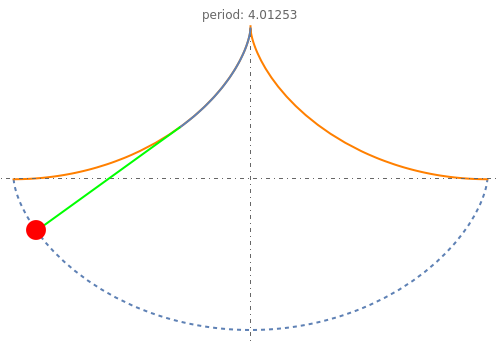
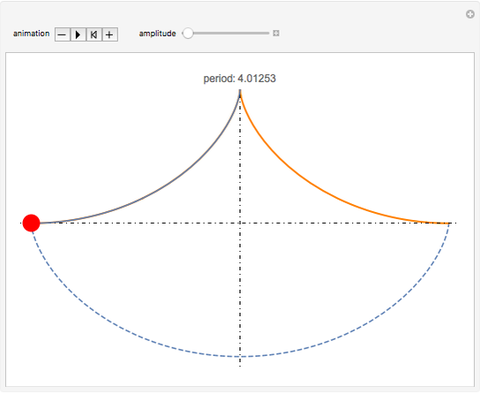
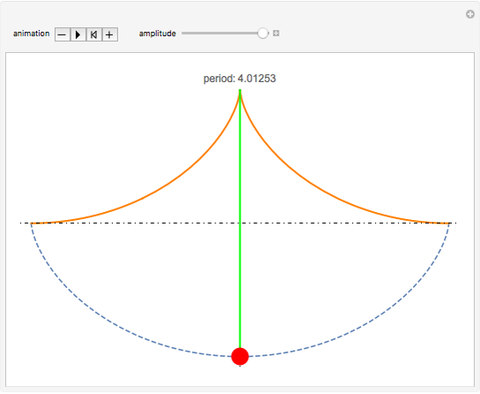
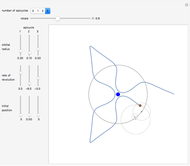
This Demonstration illustrates the isochronous movement of the cycloidal (tautochrone) pendulum.
[more]
Contributed by: Erik Mahieu (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
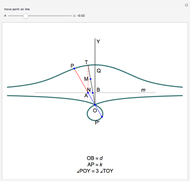
Considered here is a simple pendulum consisting of a bob, idealized as a point mass, attached to a pivot point by a massless string having fixed length  . The pendulum is assumed to be subject only to gravity.
. The pendulum is assumed to be subject only to gravity.
The path of the bob is the cycloid formed by a circle of radius 1 running from  to
to  , passing through the point
, passing through the point  . With
. With  as the angle through which the circle has rolled by time
as the angle through which the circle has rolled by time  , this cycloid is given by the parametric equation
, this cycloid is given by the parametric equation
 .
.
Using Lagrangian dynamics, we have 
and the resulting equation of motion is  .
.
The period of a cycloidal pendulum is  for any amplitude. With
for any amplitude. With  , the period is 4.01213. In this Demonstration, the function period[amplitude] verifies this fact by escaping NDSolve with the "EventLocator" method at the point where the pendulum passes the vertical.
, the period is 4.01213. In this Demonstration, the function period[amplitude] verifies this fact by escaping NDSolve with the "EventLocator" method at the point where the pendulum passes the vertical.
Much more information about the Huygens clock can be found in the following reference.
Reference
[1] A. Emmerson. "Things Are Seldom What They Seem — Christiaan Huygens, the Pendulum and the Cycloid." The Horological Foundation. (2010) www.antique-horology.org/Piggott/RH/Images/81V_Cycloid.pdf.
Permanent Citation