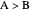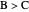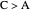Dice Transitivity

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
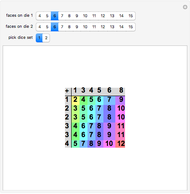
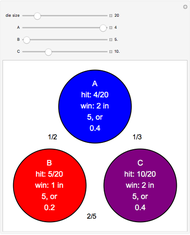
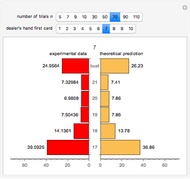
Roll dice  and
and  with the higher die winning. In terms of advantage, the possibilities are
with the higher die winning. In terms of advantage, the possibilities are  (equality),
(equality), 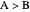 or
or  .
.
Contributed by: Ed Pegg Jr (December 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
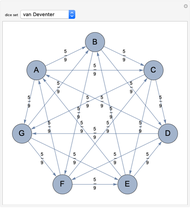
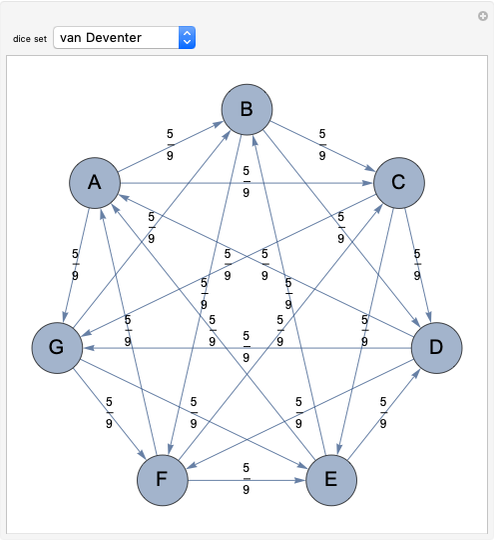
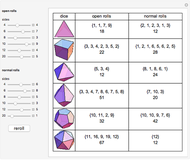
Oskar van Deventer developed the set
{{2,14,17},{7,10,16},{5,13,15},{3,9,21},{4,11,18},{6,8,19},{1,12,20}}.
Eric Harshbarger developed the "Go First 4" dice. Whether there is a "Go First 5" set on 60-sided dice is unsolved.
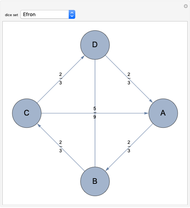
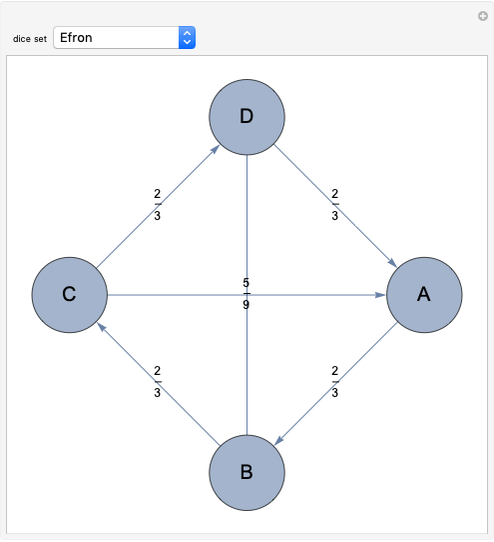
Bradley Efron developed the set
{{4,4,4,4,0,0},{3,3,3,3,3,3},{6,6,2,2,2,2},{5,5,5,1,1,1}}.
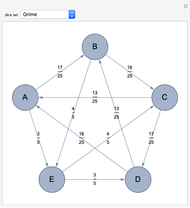
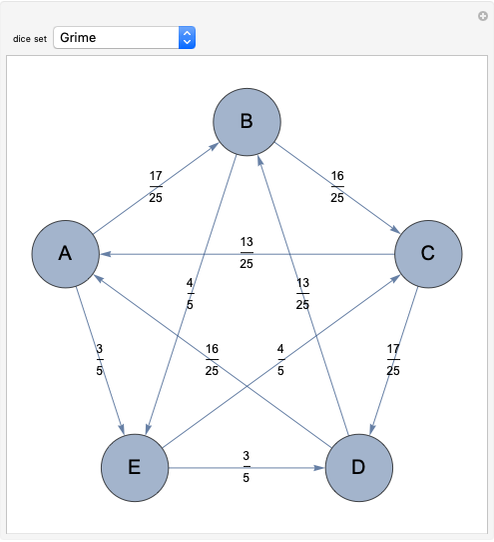
James Grime developed the set
{{2,2,7,7,7},{1,6,6,6,6},{4,4,4,4,9},{3,3,3,8,8},{5,5,5,5,5}}.
References
[1] E. Pegg Jr, "Tournament Dice," Math Games. (Sep 24 2020) www.mathpuzzle.com/MAA/39-Tournament%20Dice/mathgames_07_ 11_05.html.
[2] E. Harshbarger. "Go First Dice." (Sep 24, 2020) www.ericharshbarger.org/dice/go_first_dice.html.
[3] M. Gardner, "Nontransitive Paradoxes," Time Travel and Other Mathematical Bewilderments, New York: W. H. Freeman, 1988.
[4] M. Gardner, "Nontransitive Dice and Other Probability Paradoxes," Wheels, Life, and Other Mathematical Amusements, New York: W. H. Freeman, 1983.
Permanent Citation