Wolfram Demonstrations Project

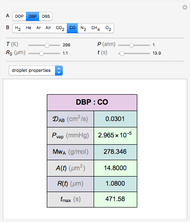
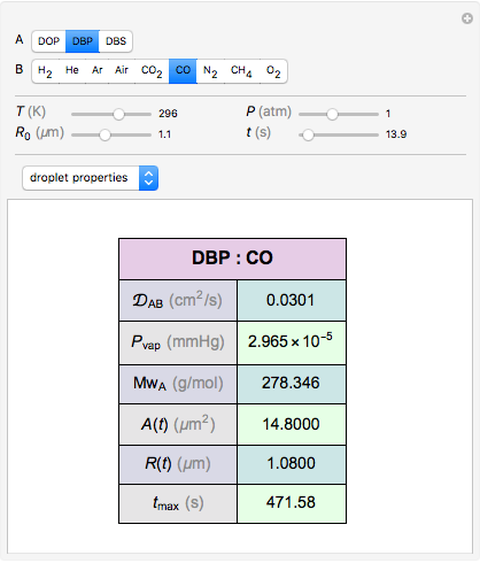
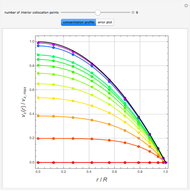
Diffusion-controlled evaporation of aerosol droplets in an ambient gas is important in various engineering and scientific fields, such as premixing air and fuel, ink-jet printing, spraying of pesticides, biochemical assays, and atmospheric pollution. For isothermal, quasi-steady evaporation, Maxwell [1], showed that the time rate of change of the droplet radius

is given by

where

is the binary diffusion coefficient for the vapor molecules of species

in a surrounding continuous phase

is the vapor pressure of species

is the molecular weight of species

, and

is its density. The quantities

and

are the temperature of the surrounding phase and the universal gas constant, respectively. Under isothermal conditions the surface area

of the evaporating drop is given by

, where

The binary diffusion coefficients can be predicted from the kinetic theory of gases using the Chapman–Enskog theory with a Lennard–Jones (6-12) potential [2]. The vapor pressure of species

at temperature

can be related to a reference temperature

by applying the Clausius–Clapeyron equation:

where

is the heat of vaporization of species

In this Demonstration you can select an aerosol compound

from a family of commonly used plasticizers that have low vapor pressures: DOP (dioctyl phthalate), DBP (dibutyl phthalate), and DBS (dibutyl sebacate). The necessary thermodynamic properties for the plasticizers are taken from [3]. You can also select species

for the surrounding gas phase. Using the sliders, you can specify the temperature

, the pressure

of the surrounding gas phase, the initial aerosol droplet radius

, and the evaporation time

. Then using the pull-down menu you can view: (1) a plot of

versus

; (2) an image of the drop (relative to its initial size) at a specified evaporation time

; and (3) the droplet properties displayed in tabular form at time

. Note:

in the droplet properties table denotes the evaporation time such that

. To accommodate the wide range of

values for different diffusion experiments, the evaporation time slider is reset to

when any of the other controls are changed.

Contributed by: Brian G. Higgins and Housam Binous

Slider Zoom

References

[1] J. C. Maxwell, The Scientific Papers of James Clerk Maxwell, Vol. II, (W. D. Niven, ed.), Cambridge, England: Cambridge University Press, 1890 p. 625. archive.org/details/scientificpapers02maxwuoft.

[2] R. B. Bird, W. E. Stewart, and E. N. Lightfoot, Transport Phenomena, 2nd ed., New York: John Wiley & Sons, 2002.

[3] A. K. Ray, E. J. Davis, and P. Ravindran, "Determination of Ultra-Low Vapor Pressures by Submicron Droplet Evaporation," Journal of Chemical Physics 71(2), 1979 pp. 582–587. doi:10.1063/1.438408.

Contributed by: Brian G. Higgins and Housam Binous

"Diffusion-Controlled Evaporation of an Aerosol Droplet"
http://demonstrations.wolfram.com/DiffusionControlledEvaporationOfAnAerosolDroplet/
Wolfram Demonstrations Project
Published: February 27, 2013