The Györgyi-Field Model for the Belousov-Zhabotinsky Reaction

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
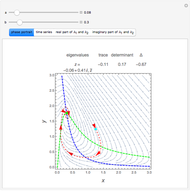
The Belousov–Zhabotinsky (BZ) reaction in a continuous-flow stirred-tank reactor (CSTR) can exhibit chaos, contrary to the Oregonator model, which has no chaotic solutions.
[more]
Contributed by: Housam Binous, Brian G. Higgins, and Ahmed Bellagi (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
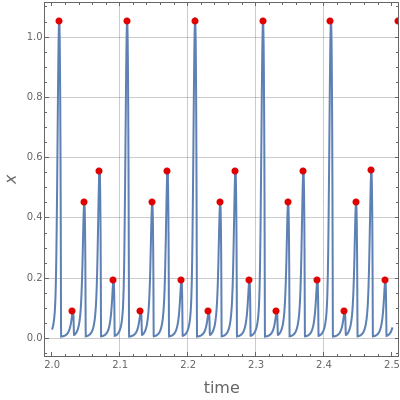
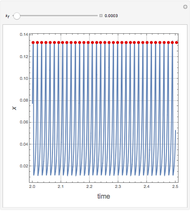
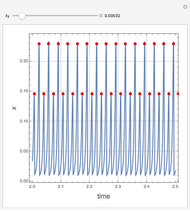
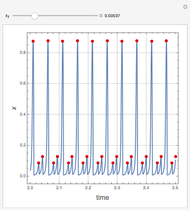
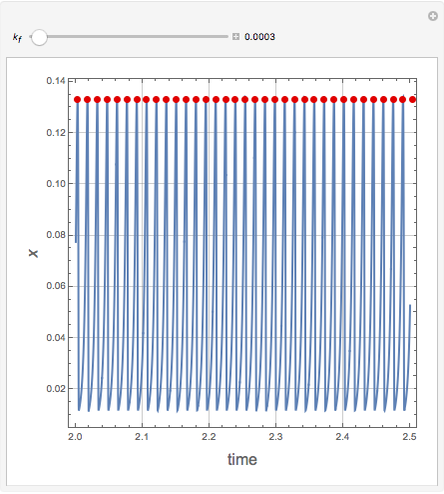
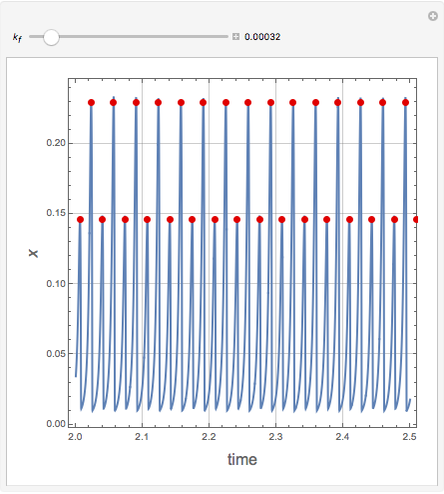
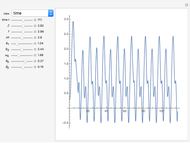
The snapshots show several situations.
Snapshot 1: periodic behavior for 
Snapshot 2: period-2 for 
Snapshot 3: period-3 for 
Snapshot 4: period-5 for 
Snapshot 5: chaos for 
Snapshots 6 and 7: finally back to period-2 and periodic behavior for  and
and  , respectively.
, respectively.
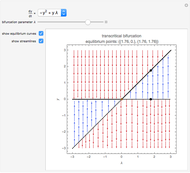
This bifurcation diagram (a remerging Feigenbaum tree) given below was obtained by the authors using a separate program that draws on the present Demonstration. A close look at this bifurcation diagram confirms the findings seen in the various snapshots given above.

References
[1] L. Györgyi and R. J. Field, "A Three-Variable Model of Deterministic Chaos in the Belousov-Zhabotinsky Reaction," Nature, 355, 1992 pp. 808–810. doi:10.1038/355808a0.
[2] A. Barnett, "Math 53: Chaos! - Fall 2011." (Jan 14, 2013) www.math.dartmouth.edu/~m53f11.
Permanent Citation