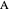Reaction-Diffusion Equations for an Autocatalytic Reaction

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
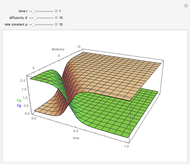
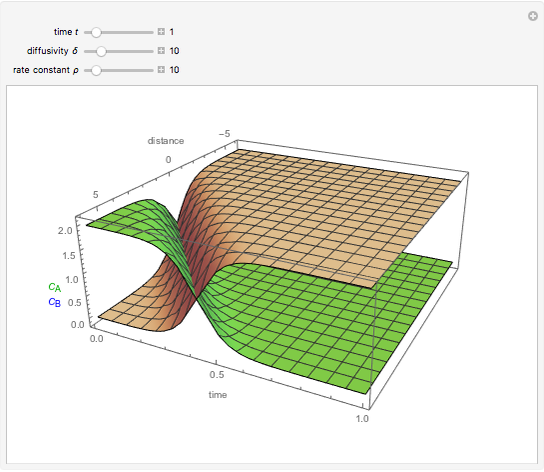
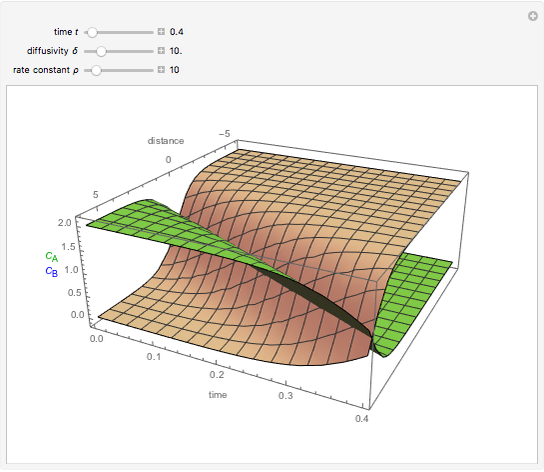
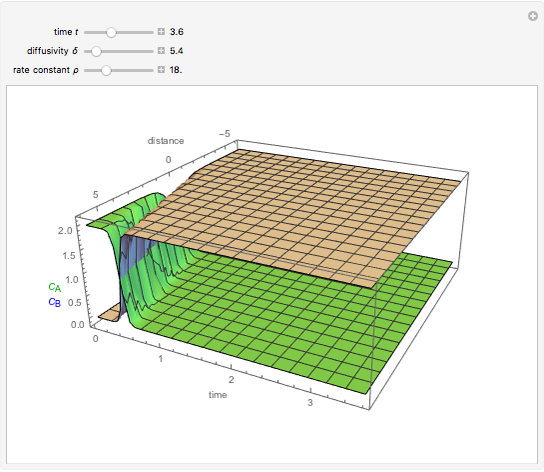
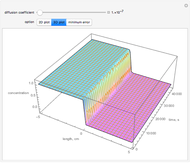
This Demonstration shows the behavior of a reaction-diffusion system in which an autocatalytic reaction takes place.
[more]
Contributed by: Clay Gruesbeck (March 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The governing equations are

and
 .
.
With the membrane at  , the initial conditions are
, the initial conditions are
 ,
,
and
 ,
with boundary conditions
,
with boundary conditions
 at
at  and
and  .
Here
.
Here  and
and  are the diffusion coefficients of
are the diffusion coefficients of  and
and  , respectively,
, respectively,  is distance, and
is distance, and  is time.
is time.
The system can be simplified by making the transformations
 and
and 
to obtain the system
 ,
,
 ,
,
which has the following analytical solution when  [1]:
[1]:
 ,
,
 ,
,
with
 , where
, where 
 is a free parameter taken as
is a free parameter taken as  .
.
Reference
[1] A. H. Salas, L. J. Martinez H., and O. Fernandez S., "Reaction-Diffusion Equations: A Chemical Application," Scientia et Technica, 17(46), 2010 pp. 134–137. www.redalyc.org/pdf/849/84920977041.pdf.
Permanent Citation