Dynamic Behavior of a Nonisothermal Chemical System

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
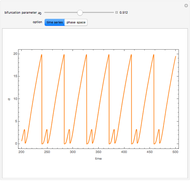
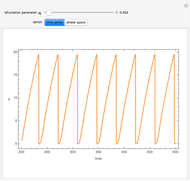
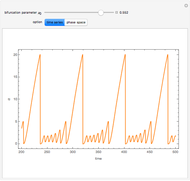
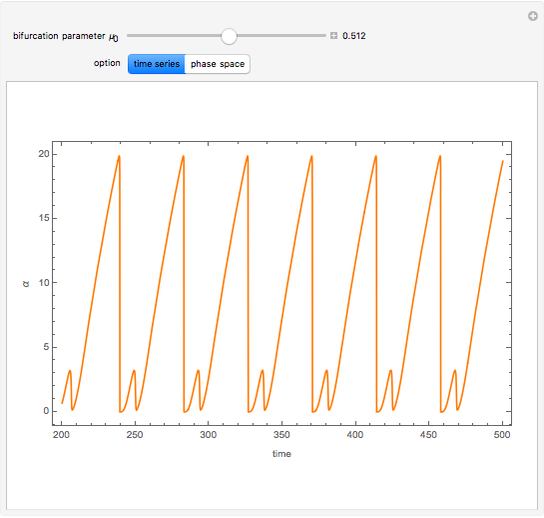
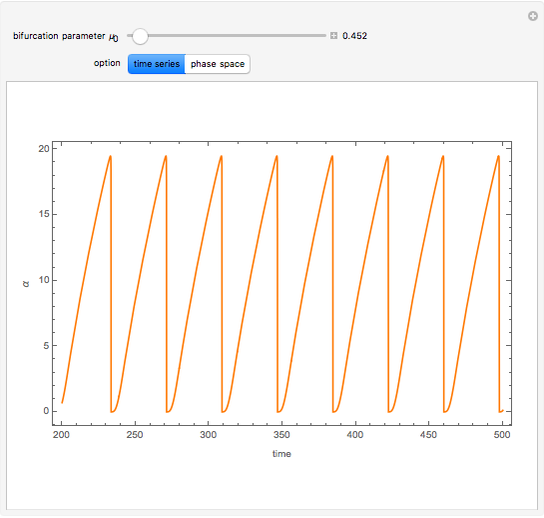
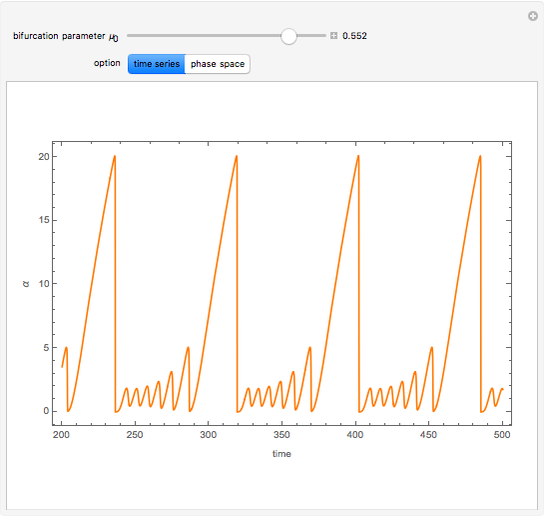
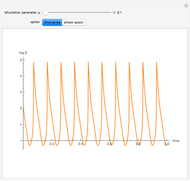
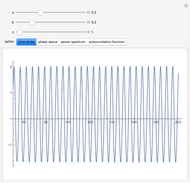
A nonisothermal chemical system displays interesting dynamic behavior ranging from period-one oscillations to period doubling and chaos, depending on the value of the bifurcation parameter,  .
.
Contributed by: Housam Binous and Zakia Nasri (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The following nonisothermal reaction system is theoretical. The steps are as follows:

Here  is a chemical precursor with constant concentration,
is a chemical precursor with constant concentration,  is the final product,
is the final product,  and
and  are intermediate chemical species,
are intermediate chemical species, 
 ,
,  and
and  are rate constants for the reactions, and
are rate constants for the reactions, and  ,
,  , and
, and  are the concentrations of the hypothetical chemical species
are the concentrations of the hypothetical chemical species  ,
,  , and
, and  .
.
The autocatalytic reaction is the following step:  , with
, with  catalyzing its own formation. This step introduces the nonlinear term
catalyzing its own formation. This step introduces the nonlinear term  in the governing equations.
The last reaction, B → C + Heat is exothermic. The rate constant of the first reaction,
P → A, follows the Arrhenius rate-law. Thus
in the governing equations.
The last reaction, B → C + Heat is exothermic. The rate constant of the first reaction,
P → A, follows the Arrhenius rate-law. Thus  depends on the temperature.
depends on the temperature.
The governing equations for the two intermediate species and the temperature are usually written in the form:
 ,
,
 ,
,
 .
.
The dimensionless governing equations are:
 ,
,
 ,
,
 .
Here
.
Here  ,
,  , and
, and  are dimensionless concentrations of
are dimensionless concentrations of  ,
,  , and the dimensionless temperature, and the four parameters
, and the dimensionless temperature, and the four parameters  ,
,  ,
,  , and
, and  depend on the rate constants of the individual reactions
depend on the rate constants of the individual reactions  ,
,  ,
,  , and
, and  , the concentration of the precursor
, the concentration of the precursor  , the molar density
, the molar density  , the molar heat capacity
, the molar heat capacity  , the surface heat transfer coefficient
, the surface heat transfer coefficient  , the surface area
, the surface area  , the surrounding temperature
, the surrounding temperature  , the heat of reaction
, the heat of reaction  for the reaction
for the reaction  , and the activation energy
, and the activation energy  of the reaction
of the reaction  .
.
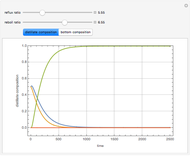
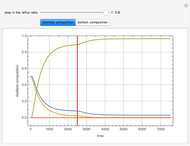
The Demonstration illustrates the dynamics of the concentrations  ,
,  , and the temperature
, and the temperature  for various values of the bifurcation parameter
for various values of the bifurcation parameter  . Choose "time series" to get a plot of
. Choose "time series" to get a plot of  versus time or "phase space" to get a three-dimensional parametric plot of
versus time or "phase space" to get a three-dimensional parametric plot of  .
.
For  = 0.5586, the
= 0.5586, the  phase-space graph is that of a spiral attractor.
phase-space graph is that of a spiral attractor.
Reference: S. K. Scott and A. S. Tomlin, "Period Doubling and Other Complex Bifurcations in Non-isothermal Chemical Systems," Philosophical Transactions of the Royal Society of London, Series A: Mathematical and Physical Sciences, 332(1624), 1990 pp. 51–68.
Permanent Citation