Wolfram Demonstrations Project

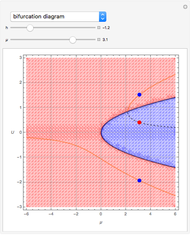
This Demonstration shows how one can compute the bifurcation diagram for a nonlinear chemical system such as the three-variable autocatalator (see Details).

Indeed, in order to obtain such a diagram, one has to locate the maxima of the time series for all values of the bifurcation parameter,

, which can be readily done using Mathematica's built-in function FindArgMax.

The Demonstration illustrates the dynamics of the concentrations

, and

for various values of the bifurcation parameter

. The time series option gives a plot of

versus time and shows the loci of all maxima.

Try the following values of

: 0.1, 0.14, 0.15, 0.151, and 0.155 to observe period 1, 2, 4, 8, and 5 behaviors, respectively. For

, chaotic behavior occurs. When

is large enough, you can observe a reversed sequence leading back to period 1 behavior. These results are confirmed by the bifurcation diagram (a remerging Feigenbaum tree), first given in [1] and reproduced in the present Demonstration.

Contributed by: Housam Binous, Zakia Nasri, and Brian G. Higgins

Slider Zoom
Automatic Animation

Consider a chemical reaction such as the shift conversion:

. To study its chemical kinetics, it is written in abstract form as

. The rate of this reaction is given by

, where

is the rate constant and

, and

are the concentrations of the species

, and

Hypothetically, the autocatalator's steps are the following:

Here

is a precursor with constant concentration,

is the final product,

, and

are intermediate chemical species,

, and

are rate constants for the individual reactions, and

, and

are the concentrations of the hypothetical chemical species

, and

This hypothetical reaction scheme is a model for a three-variable autocatalator. The autocatalytic reaction occurs in the step

, with

catalyzing its own formation. This step introduces the nonlinear term

in the governing equations, necessary in order to obtain sufficient complexity for chaos to occur.

The rate equations for the three intermediate species can be written in the form:

The corresponding dimensionless rate equations are:

,
where

, and

are the dimensionless concentrations of

, and

, and the four parameters

, and

depend on the rates of the individual reactions and the concentration of the precursor.

This is the bifurcation diagram:

Reference

[1] B. Peng, S. K. Scott, and K. Showalter, "Period Doubling and Chaos in a Three-Variable Autocatalator," The Journal of Physical Chemistry, 94(13), 1990 pp. 5243–5246.

Improved Computation of the Bifurcation Diagram for the Three-Variable Autocatalator (Wolfram Library Archive)

"Bifurcation Diagram for the Three-Variable Autocatalator" from the Wolfram Demonstrations Project
http://demonstrations.wolfram.com/BifurcationDiagramForTheThreeVariableAutocatalator/

Contributed by: Housam Binous, Zakia Nasri, and Brian G. Higgins