Eigenvalues for a Pure Quartic Oscillator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The oscillator with a quartic anharmonicity, with Hamiltonian
[more]
Contributed by: S. M. Blinder (March 2019)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The ladder operators can be defined by
 ,
,
 ,
,
with an adjustable parameter  introduced. The nonvanishing matrix elements of the Hamiltonian can then be computed, giving
introduced. The nonvanishing matrix elements of the Hamiltonian can then be computed, giving
 ,
,
 ,
,
 .
.
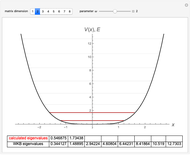
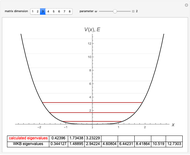
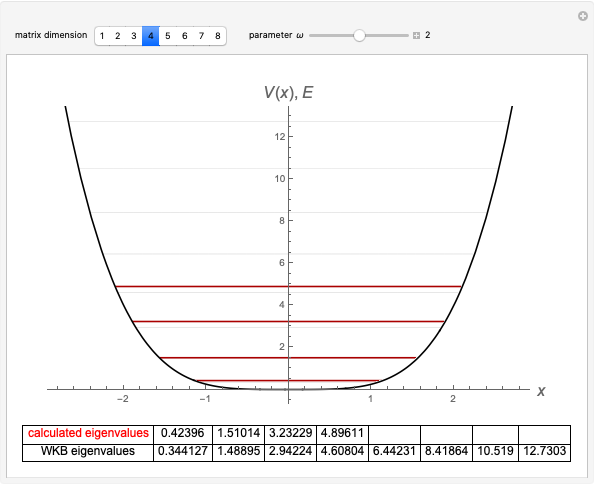
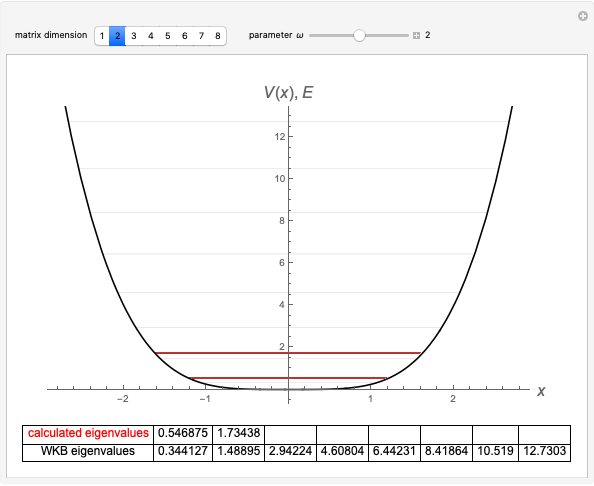
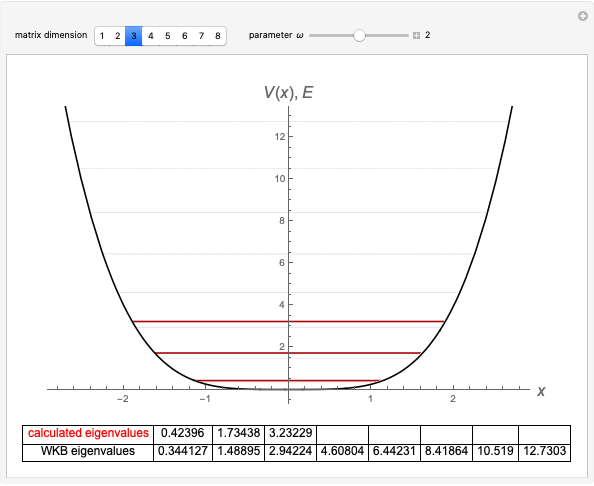
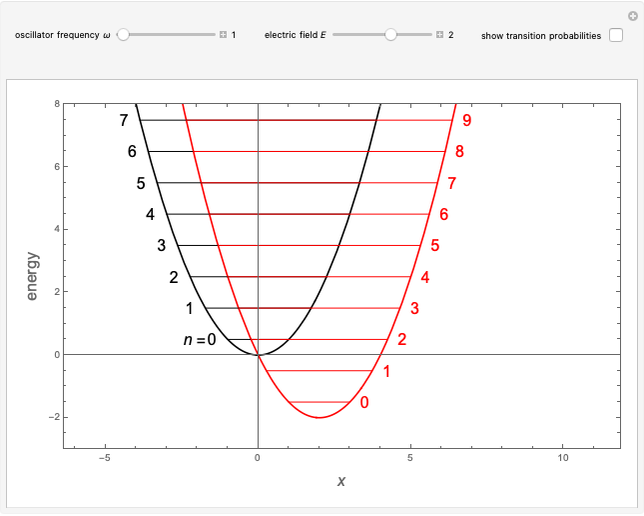
The eigenvalues are then determined using the built-in Wolfram Language function Eigenvalues for selected dimensions 1 to 8.
The WKB method determines the eigenvalues using the integral  . The resulting energies are given by
. The resulting energies are given by  .
.
A classical realization of a quartic oscillator can be approximated by a particle attached to two Hooke's law springs [3].
References
[1] P. M. Mathews, M. Seetharaman, S. Raghavan and V. T. A. Bhargava, "A Simple Accurate Formula for the Energy Levels of Oscillators with a Quartic Potential," Physics Letters A, 83(3), 1981 pp. 118–120. doi:10.1016/0375-9601(81)90511-9.
[2] S. M. Blinder, "Ammonia Inversion Energy Levels Using Operator Algebra." arxiv.org/abs/1809.08178.
[3] M. Alexander. "The Quartic Oscillator in Classical Physics." (Feb 21, 2019) www2.chem.umd.edu/groups/alexander/chem691/Quartic_oscillator.pdf.
Permanent Citation