Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Schwinger's Oscillator Model for Angular Momentum

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

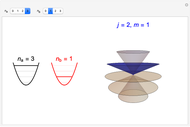
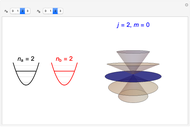
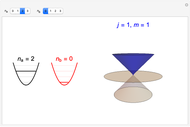
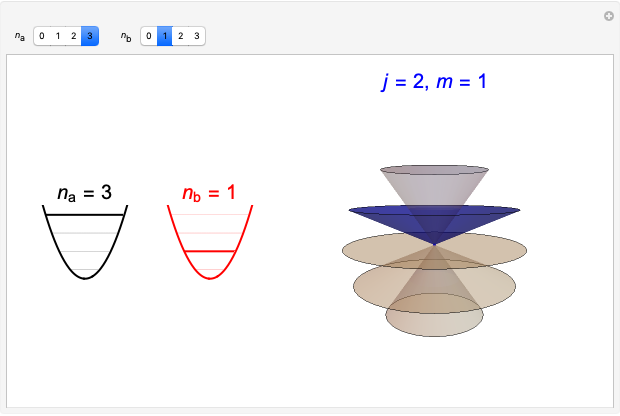
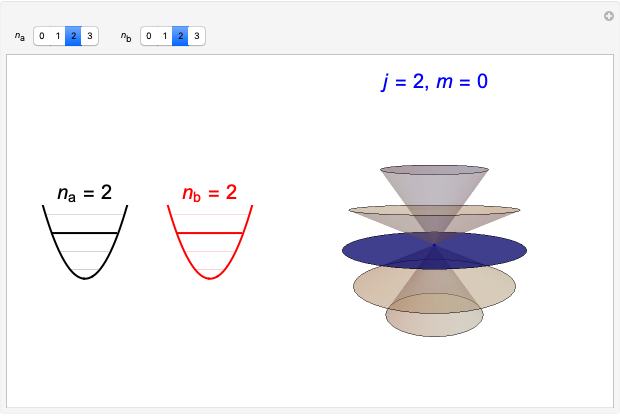
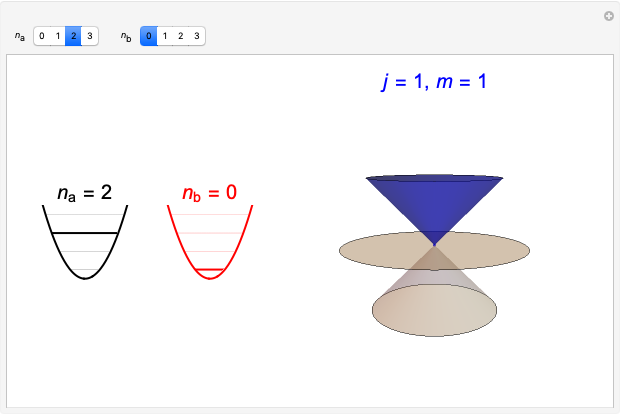
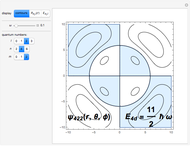
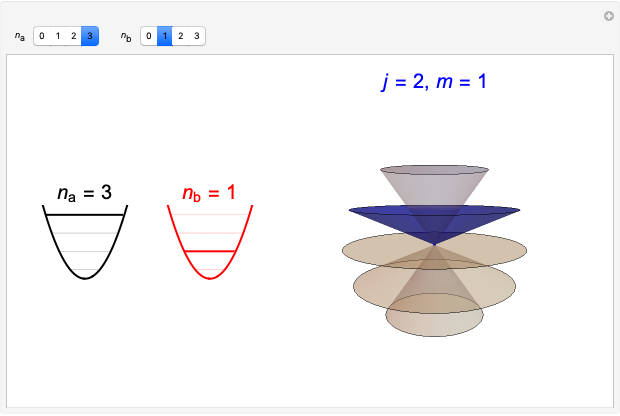
In an internal Atomic Energy Commission document published in 1952 [1], Julian Schwinger developed the quantum theory of angular momentum from the commutation relations for a pair of independent harmonic oscillators. This work has since been subsequently quoted many times [2, 3]. A simplified version of the derivation is given in the Details. This Demonstration shows the angular momentum states 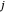, 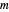derived from the quantum numbers 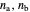for a pair of harmonic oscillators, with .

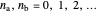Contributed by: S. M. Blinder (February 2020)
Open content licensed under CC BY-NC-SA

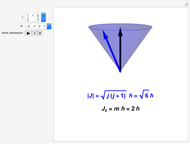
Snapshots

Details

A pair of uncoupled harmonic oscillators, designated a and b, can be defined by raising and lowering operators with commutation relations

, .

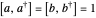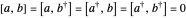It can then be shown that the operators

, ,

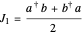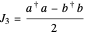
obey the canonical commutation relations for angular momentum:

, , , .

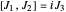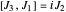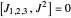The number operators for the two oscillators are given by

, , ,

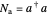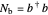with corresponding eigenvalues 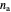, , 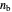, 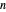each equal to an integer .

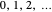In terms of the number operators, relevant angular momentum operators can be expressed as

, .

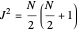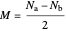The quantum number 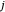evidently can be identified with 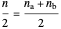, with possible values 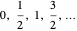. Analogously, 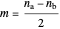, running from 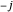to 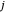in integer steps.

References

[1] J. Schwinger, "On Angular Momentum," U. S. Atomic Energy Commission Report NYO-3071, January 26, 1952. www.osti.gov/biblio/4389568.

[2] J. J. Sakurai, Modern Quantum Mechanics, Menlo Park, CA: Benjamin/Cummings, 1985 pp. 217–221.

[3] H. Verma, T. Mitra and B. P. Mandal, "Schwinger's Model of Angular Momentum with GUP." arxiv.org/abs/1808.00766.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send