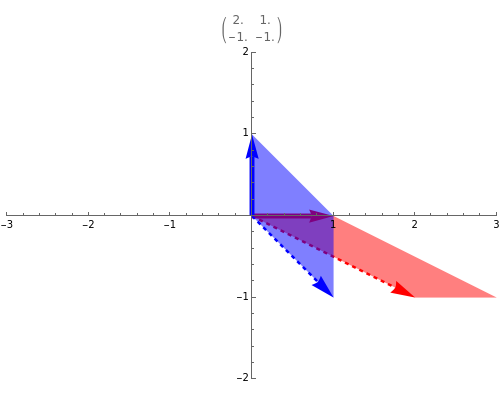
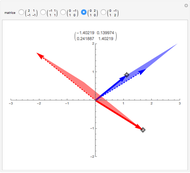
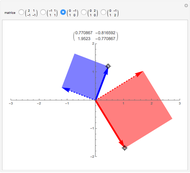
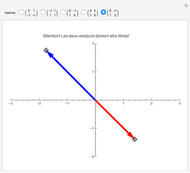
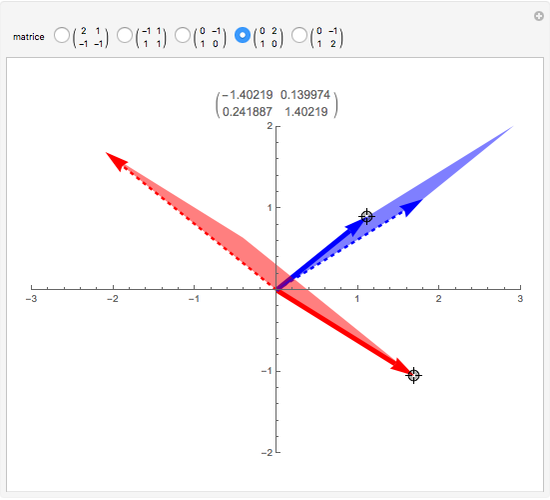
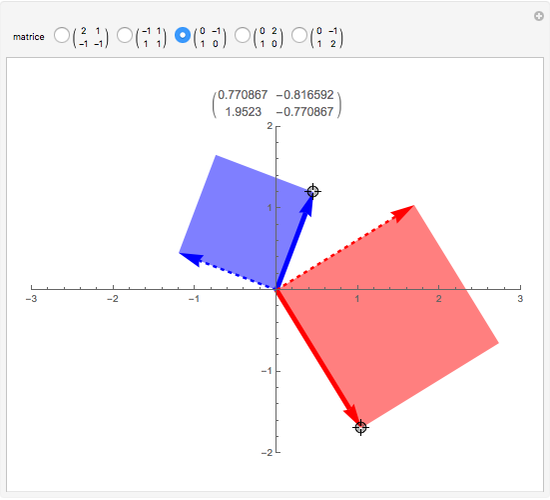
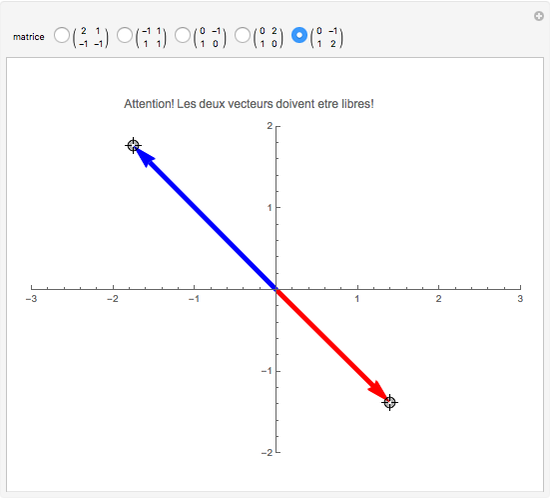
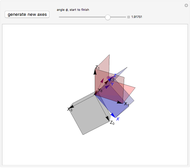
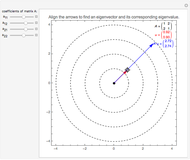
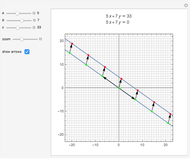
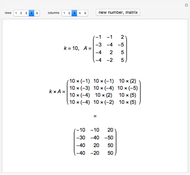
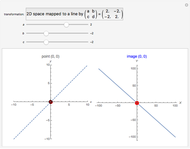
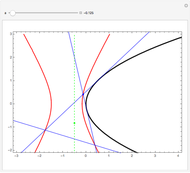
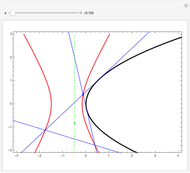
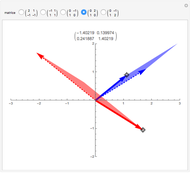
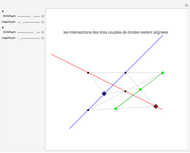
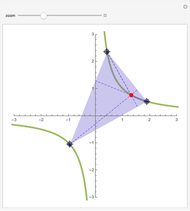
Une application linéaire transforme des vecteurs en d'autres vecteurs. On dit qu'un vecteur non nul (ici en gras) est un vecteur propre quand son image (ici en pointillés) est un multiple de lui-même, ce qui correspond au cas où le parallélogramme disparaît. Cette Démonstration permet de trouver par tâtonnements une base de vecteurs propres d'une application, tout en montrant que la matrice de l'application devient diagonale dans cette nouvelle base.
Le but de la manipulation est de faire disparaître les parallélogrammes, i.e., de parvenir à deux vecteurs propres indépendants. Dans ce cas, la matrice devient diagonale, i.e., les termes non diagonaux sont nuls. Pour certaines des matrices proposées, cela est impossible.
Quand on a trouvé un vecteur propre, on peut l'étirer dans sa propre direction—il restera vecteur propre—et aussi observer qu'est-ce qui reste inchangé dans la matrice.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
