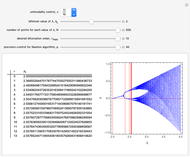
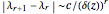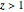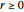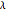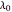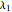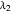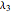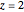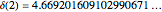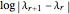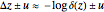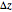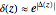Estimating the Feigenbaum Constant from a One-Parameter Scaling Law

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
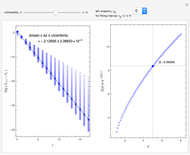
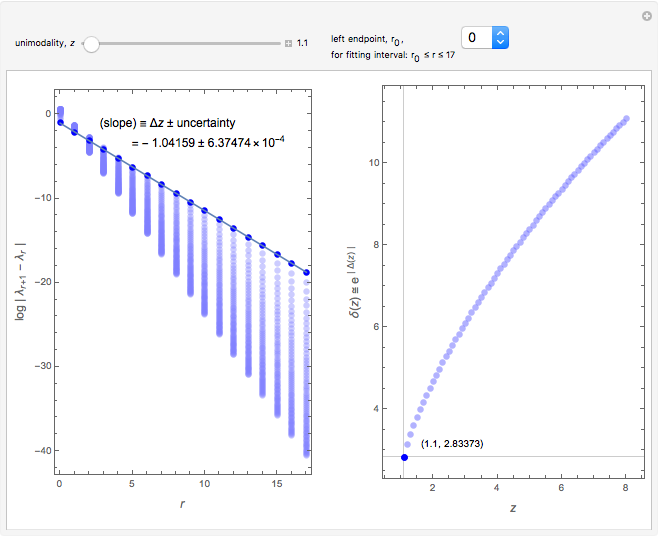
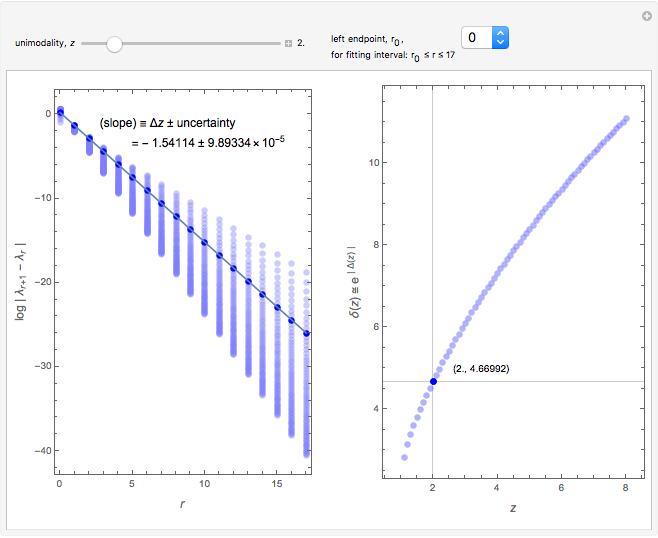
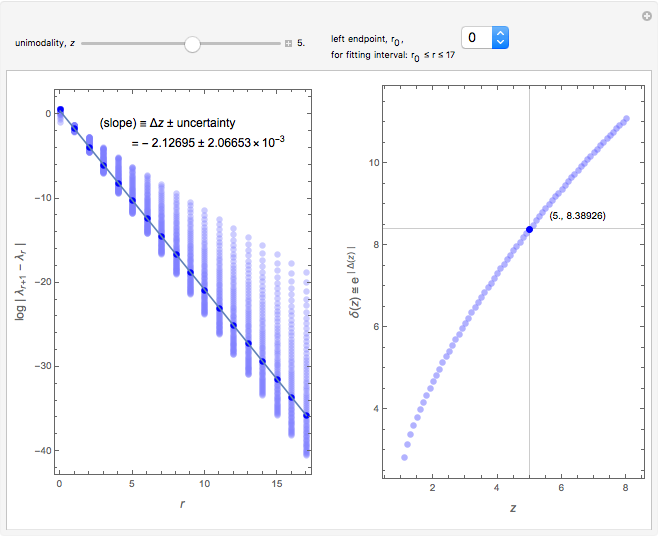
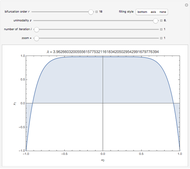
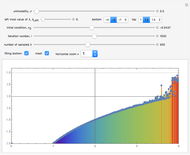
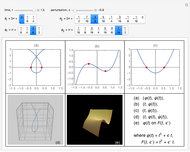
Mitchell J. Feigenbaum's one-parameter scaling law for one-dimensional iterative maps with  -unimodality is given by
-unimodality is given by
Contributed by: Ki-Jung Moon (December 2013)
Open content licensed under CC BY-NC-SA
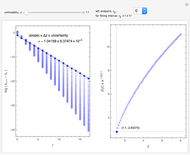
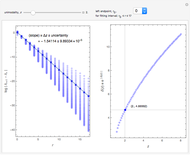
Snapshots
Details
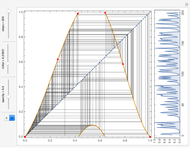
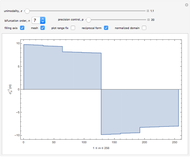
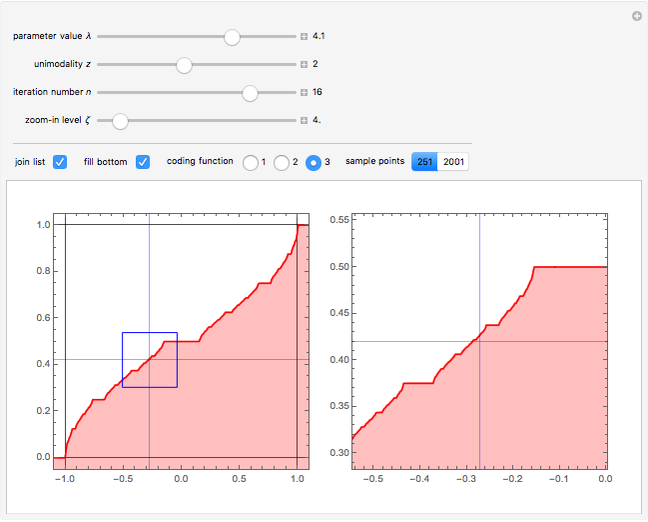
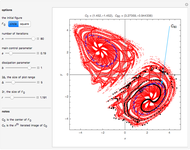
1. The test map used in this Demonstration, 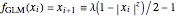 [8, 9], generalizes the well-known logistic map
[8, 9], generalizes the well-known logistic map 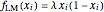 [3–7].
[3–7].
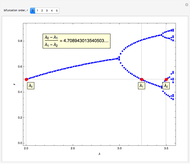
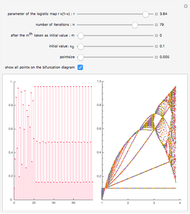
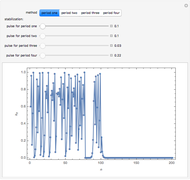
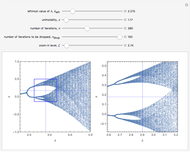
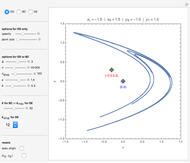
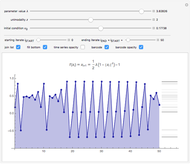
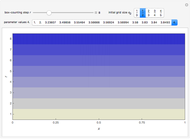
2. The program for this Demonstration presents a large collection of super-stable parameter values (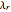 ) for period-doubling periodic attractors within
) for period-doubling periodic attractors within 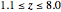 and
and 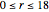 , which were obtained using a high-precision Newton algorithm [10] with fixed precision 50 [11]. These values are accurate up to 45 decimal places, so you can use them for your own research or study.
, which were obtained using a high-precision Newton algorithm [10] with fixed precision 50 [11]. These values are accurate up to 45 decimal places, so you can use them for your own research or study.
3. Keith Briggs calculated precise values of 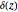 for
for 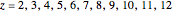 in his 1997 thesis [12]. For even
in his 1997 thesis [12]. For even  , the estimated values of
, the estimated values of 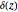 in this Demonstration are consistent with his calculation. But, for odd
in this Demonstration are consistent with his calculation. But, for odd  , the estimated values are slightly different from his calculation. It would be nice if someone could explain this. Refer to the following table for comparison:
, the estimated values are slightly different from his calculation. It would be nice if someone could explain this. Refer to the following table for comparison:
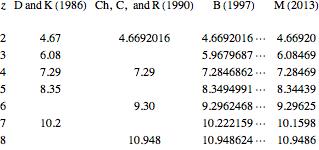
Here D and K refers to for Delbourgo and Kenny's calculation [13]; Ch, Cv, and R for Christiansen, Cvitanović, and Rugh's calculation [14]; B for Briggs' calculation; and M for the calculation in this Demonstration for the fitting interval 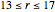 .
.
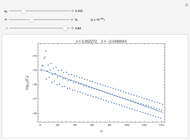
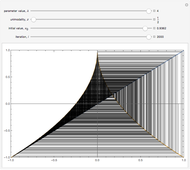
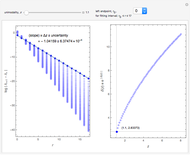
4. Of particular interest is that the following limits exist:
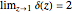 [15],
[15],
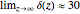 [16–18].
[16–18].
References
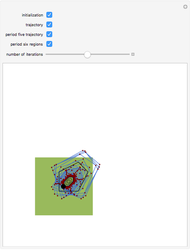
[1] A parameter value is called "super-stable (or super-attracting)" if its ω-limit set contains at least one critical point of an iterative map.
[2] In mathematics, specifically bifurcation theory, the Feigenbaum constants are two mathematical constants that both express ratios in a bifurcation diagram for a nonlinear map. They are named after the mathematician/physicist Mitchell J. Feigenbaum. The first Feigenbaum constant 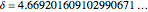 is the limiting ratio of each bifurcation interval to the next between every period doubling of iterative maps with degree-2 unimodality. The second Feigenbaum constant
is the limiting ratio of each bifurcation interval to the next between every period doubling of iterative maps with degree-2 unimodality. The second Feigenbaum constant 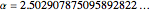 is the ratio between the width of a tine and the width of one of its two subtines (except the tine closest to the fold). Both numbers are believed to be transcendental, although they have not been proven to be so. See the related Wikipedia article, "Feigenbaum Constants." See also [3-9].
is the ratio between the width of a tine and the width of one of its two subtines (except the tine closest to the fold). Both numbers are believed to be transcendental, although they have not been proven to be so. See the related Wikipedia article, "Feigenbaum Constants." See also [3-9].
[3] M. J. Feigenbaum, "Quantitative Universality for a Class of Non-Linear Transformations," Journal of Statistical Physics, 19, 1978 pp. 25–52.
[4] M. J. Feigenbaum, "The Universal Metric Properties of Nonlinear Transformations," Journal of Statistical Physics, 21, 1979 pp. 669–706.
[5] K. T. Alligood, T. D. Sauer, and J. A. Yorke, Chaos: An Introduction to Dynamical Systems, New York: Springer, 1996.
[6] S. H. Strogatz, Nonlinear Dynamics and Chaos, Studies in Nonlinearity, New York: Perseus Books Publishing, 1994.
[7] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, 2002.
[8] K.-J. Moon, "Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Sciences, 18, 2008 pp. 023104.
[9] K.-J. Moon, "Erratum: Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Sciences, 20, 2010 pp. 049902.
[10] In numerical analysis, the Newton method (also known as the Newton–Raphson method), named after Issac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. See the related Wikipedia article, "Newton's Method."
[11] In computing, a fixed-point number representation is a real data type for a number that has a fixed number of digits below the decimal point. Fixed-point number representation can be compared to the more complicated (and more computationally demanding) floating-point number representation. See the related Wikipedia article, "Fixed-Point Arithmetic."
[12] K. Briggs, "Feigenbaum Scaling in Discrete Dynamical Systems," Ph.D. thesis, Department of Mathematics, Melbourne University, Australia, 1997. keithbriggs.info/documents/Keith_Briggs_PhD.pdf.
[13] R. Delbourgo, B. G. Kenny, "Universality Relations," Physical Review A, 33, 1986 pp. 3293–3302.
[14] F. Christiansen, P. Cvitanović, and H. H. Rugh, "The Spectrum of the Period-Doubling Operator in Terms of Cycles," Journal of Physics A, 23, 1990 pp. 713–717.
[15] P. Collet, J.-P. Eckmann, and O. E. Lanford, "Universal Properties of Maps on an Interval," Communications in Mathematical Physics, 76, 1980 pp. 211–254.
[16] J.-P. Eckmann and P. Witter, Computer Methods and Borel Summability Applied to Feigenbaum's Equations, New York: Springer–Verlag, 1985.
[17] J. P. van der Weele, H. W. Capel, and R. Kluiving, "On the Scaling Factors 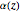 and
and 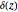 ," Physics Letters A, 119, 1986 pp. 15–20.
," Physics Letters A, 119, 1986 pp. 15–20.
[18] J. P. van der Weele, H. W. Capel, and R. Kluiving, "Period-Doubling in Maps with a Maximum of order  ," Physica A, 145, 1987 pp. 425–460.
," Physica A, 145, 1987 pp. 425–460.
Permanent Citation