Ethane Pyrolysis in a Tubular Reactor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
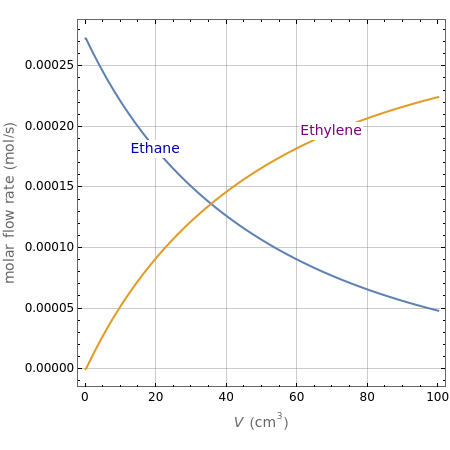
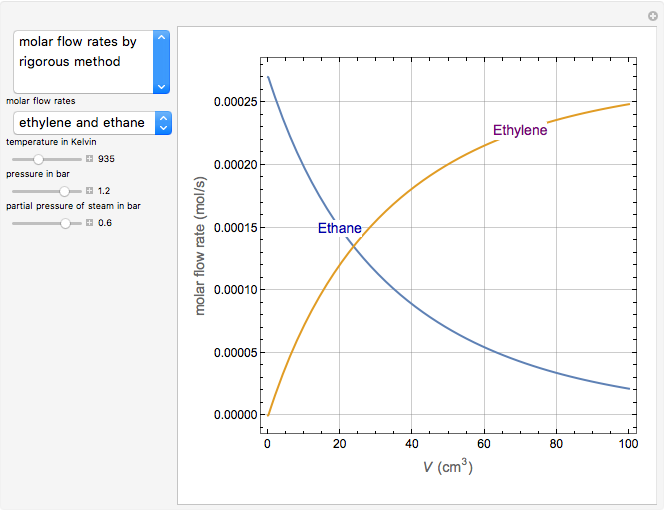
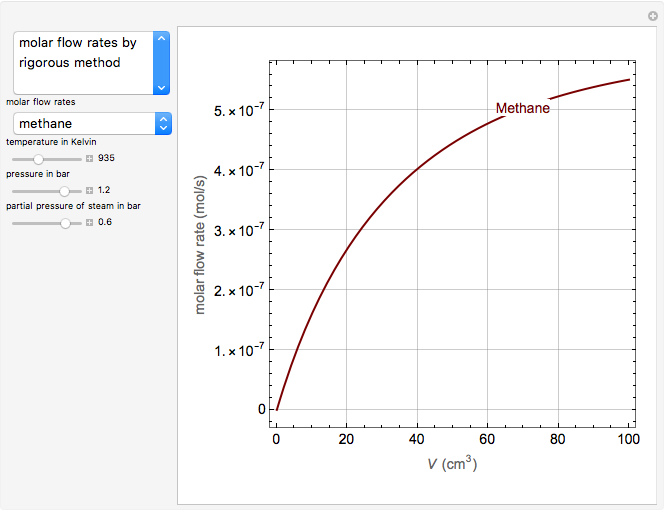
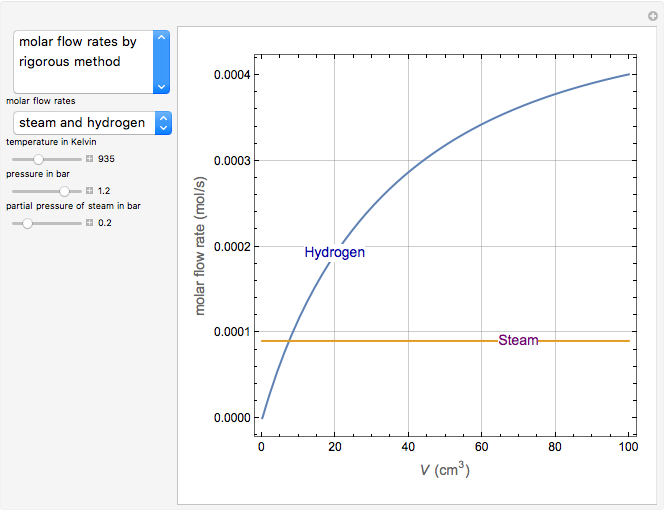
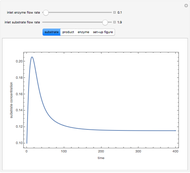
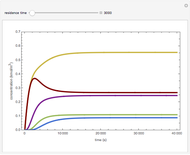
Olefin compounds such as ethylene can be produced by the pyrolysis of hydrocarbons at an elevated temperature. The olefin yield depends on the reaction temperature and the partial pressure of the hydrocarbon, which can be controlled by adding steam as a diluent. This Demonstration analyzes the isothermal pyrolysis of ethane to produce ethylene in a tubular reactor operating at steady state. The feed stream to the reactor contains ethane with steam as a diluent. The gas phase reaction is assumed to behave as an ideal gas in plug flow (no velocity gradients in the reactor). You can vary the reaction temperature, the inlet composition, and the inlet pressure. During the pyrolysis, reaction intermediates in the form of radicals are produced. The kinetics of the reaction can be simplified by assuming that the rates of production of the radical species are zero. This is known as the quasi-steady state assumption (QSSA). You can assess the validity of the QSSA by examining the rates of production profiles of the radical species along the length of the reactor (expressed in terms of reactor volume).
Contributed by: Housam Binousand Brian G. Higgins (January 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The kinetic steps for the pyrolysis reaction of ethane are
Step 1: 
Step 2: 
Step 3: 
Step 4: 
Step 5: 
In the above steps  is the methyl radical,
is the methyl radical,  is the ethyl radical, and
is the ethyl radical, and  is a hydrogen radical. The rate of reaction for each kinetic step is determined by mass action kinetics. Thus for the
is a hydrogen radical. The rate of reaction for each kinetic step is determined by mass action kinetics. Thus for the  kinetic step, the rate of reaction is
kinetic step, the rate of reaction is  , where
, where  represents the reactant species at the
represents the reactant species at the  reaction step, and
reaction step, and  is the stoichiometric coefficient of the
is the stoichiometric coefficient of the  reactant at the
reactant at the  kinetic step. The species balance for the
kinetic step. The species balance for the  species is
species is  , where
, where  is the volumetric flow rate and
is the volumetric flow rate and  is the volume of the reactor. The rate constants
is the volume of the reactor. The rate constants  are assumed to have Arrhenius dependence on temperature:
are assumed to have Arrhenius dependence on temperature:  . The values of
. The values of  are taken from [1].
are taken from [1].
Reference
[1] J. B. Rawlings and J. G. Ekerdt, Chemical Reactor Analysis and Design Fundamentals, Madison, WI: Nob Hill Publishing, 2002.
Permanent Citation