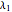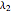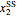Phase-Plane Analysis of a Biochemical Reactor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
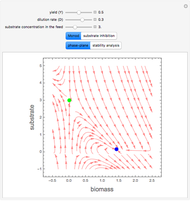
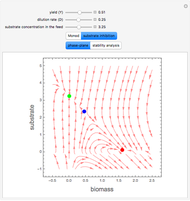
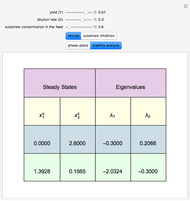
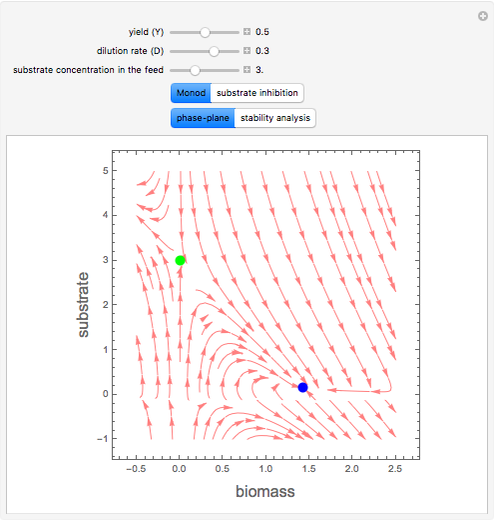
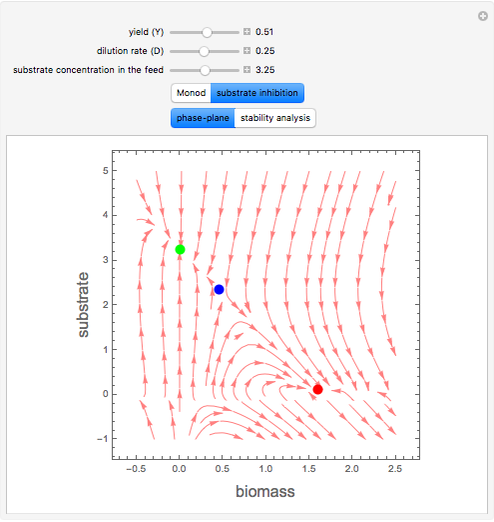
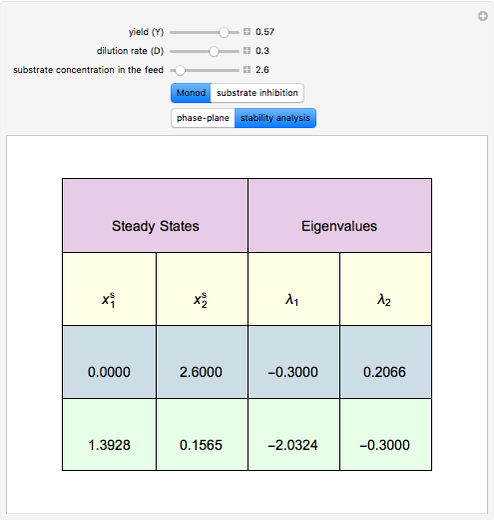
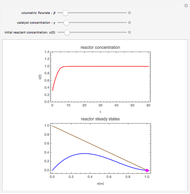
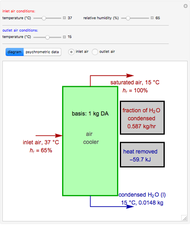
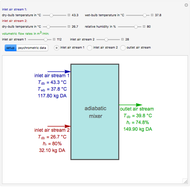
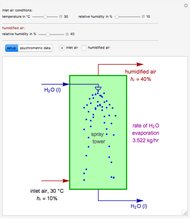
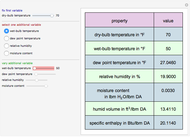
A biochemical reactor can show complex dynamic behavior, including multiple steady states. This Demonstration plots the phase-plane diagram and computes the stability of the steady states. You can choose either the Monod model or the substrate inhibition model for the growth rate expression. Parameters of the specific growth rate expression are taken from [1]. You can select numerical values for the yield, dilution rate, and substrate concentration in the feed stream.
[more]
Contributed by: Housam Binous, Brian G. Higgins, and Ahmed Bellagi (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In 1942, Monod proposed the following form of the specific growth coefficient:
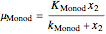 .
.
The specific growth coefficient with the substrate inhibition  is given by:
is given by:
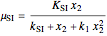 .
.
The biochemical reactor is governed by the coupled equations:
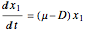 ,
,
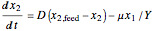 ,
,
where 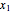 is the biomass concentration,
is the biomass concentration, 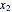 is the substrate concentration,
is the substrate concentration, 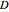 is the dilution rate,
is the dilution rate, 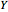 is the yield,
is the yield, 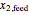 is the feed substrate concentration, and
is the feed substrate concentration, and  is the specific growth coefficient.
is the specific growth coefficient.
Here, 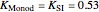 ,
, 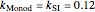 ,
, 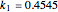 are taken from [1].
are taken from [1].
Reference
[1] B. Wayne Bequette, Process Dynamics, Modeling, Analysis, and Simulation, Upper Saddle River, NJ: Prentice Hall, 1998.
Permanent Citation