Expanded Fermi Solution to Retrodict the Initial from the Final Number in a Stochastic Process

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
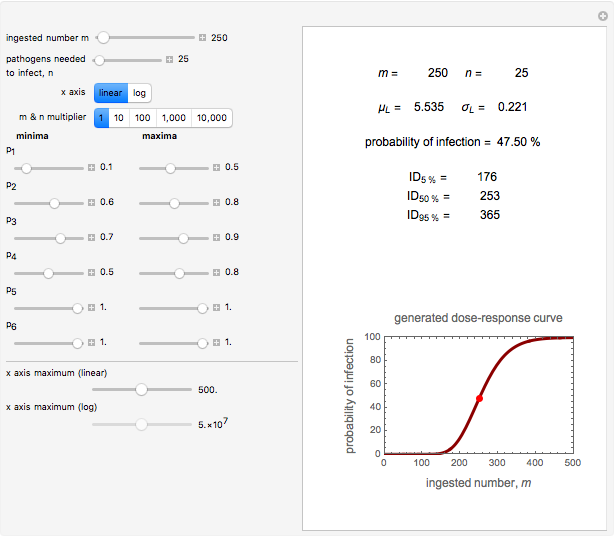
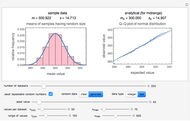
This Demonstration employs the "expanded Fermi solution" to estimate the most probable initial number of ingested microorganisms, pathogens, or probiotics that will result in a given number of survivors in the gut. The method is based on entering the ranges of the probabilities that they will survive the different stages in the digestive tract. The method can be extended to include washing, cooking, cooling, or freezing prior to ingestion. It can also be used to estimate the most probable number of dissatisfied customers given the number of received complaints, the number of defective units, and so on.
Contributed by: Mark D. Normand, Micha Peleg, and Joseph Horowitz (May 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
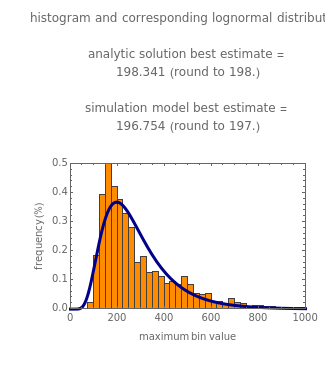
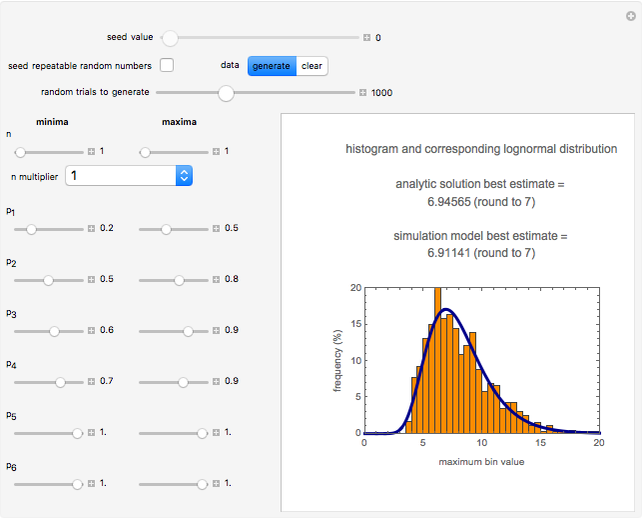
Snapshot 1: estimate of the most probable number of ingested pathogenic bacterial cells from which one will survive the passage to the gut
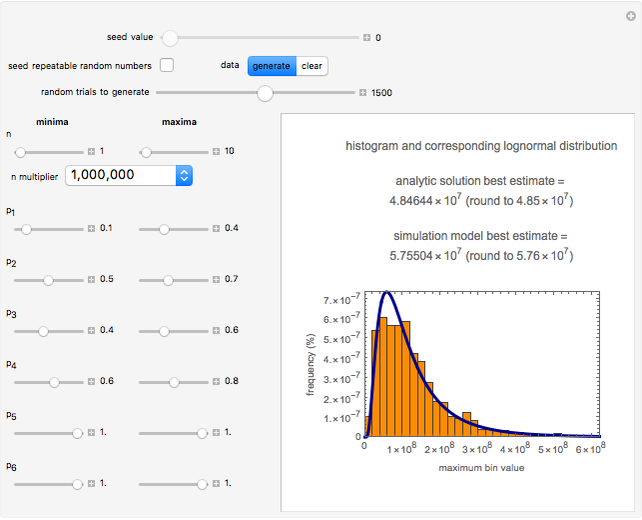
Snapshot 2: estimate of the most probable number of probiotic bacterial cells from which 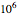 to
to 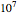 will remain viable upon reaching the gut
will remain viable upon reaching the gut
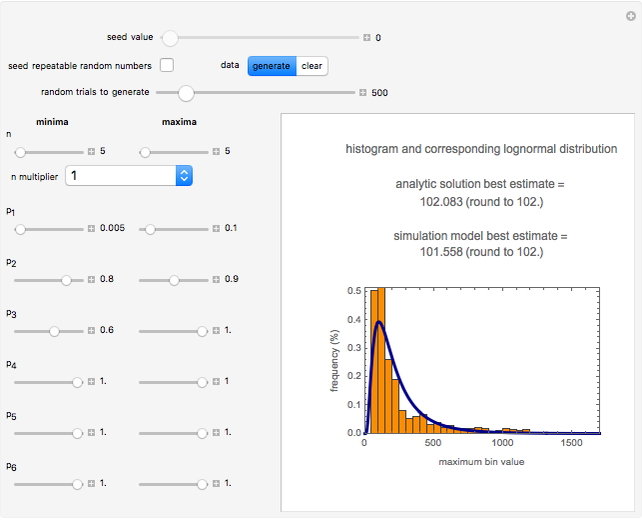
Snapshot 3: estimate of the most probable number of dissatisfied customers given that five written complaints have been received
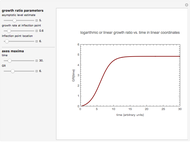
Snapshot 4: estimate of the most probable number of spores of a probiotic bacterium in a heat-processed food germinating in the gut
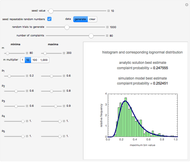
This Demonstration generates estimates of the most probable initial number of cells, customers, or units in general within the range  minimum to
minimum to  maximum set by the user with sliders and a drop-down menu. The ranges of the
maximum set by the user with sliders and a drop-down menu. The ranges of the 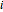 probability factors (
probability factors (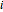 from 1 to 6) are specified by
from 1 to 6) are specified by 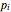 minimum and
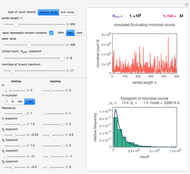
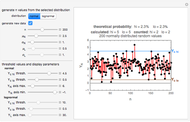
minimum and 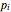 maximum and are also set by sliders. Monte Carlo simulations to determine the initial number can be done with or without a seed. Check the "seed repeatable random numbers" box to generate a repeatable random sequence from the seed selected using the "seed value" slider. The number of repeated trials is entered using the "random trials to generate" slider. The program generates a new dataset whenever the value of any control other than the clear button is altered. For a new random dataset at the current control settings, click "clear" followed by "generate". For scenarios involving fewer than all six
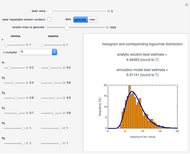
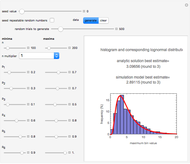
maximum and are also set by sliders. Monte Carlo simulations to determine the initial number can be done with or without a seed. Check the "seed repeatable random numbers" box to generate a repeatable random sequence from the seed selected using the "seed value" slider. The number of repeated trials is entered using the "random trials to generate" slider. The program generates a new dataset whenever the value of any control other than the clear button is altered. For a new random dataset at the current control settings, click "clear" followed by "generate". For scenarios involving fewer than all six 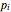 factors, set the unused factor's minimum and maximum values to 1. The panel shows the program controls at their current settings, a histogram of the estimates computed in the repeated trials, and the lognormal distribution having the same logarithmic mean and standard deviation as the generated estimates shown as a solid blue curve. The plot title text includes the analytic solution "best estimate" and the one derived from the lognormal distribution's mode. Estimates for
factors, set the unused factor's minimum and maximum values to 1. The panel shows the program controls at their current settings, a histogram of the estimates computed in the repeated trials, and the lognormal distribution having the same logarithmic mean and standard deviation as the generated estimates shown as a solid blue curve. The plot title text includes the analytic solution "best estimate" and the one derived from the lognormal distribution's mode. Estimates for 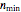 and
and 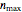 outside their sliders' allowed range of 1 to 1000 can be obtained by setting the "
outside their sliders' allowed range of 1 to 1000 can be obtained by setting the " multiplier" drop-down menu to the appropriate factor. Notice that if all seven factors' (i.e.,
multiplier" drop-down menu to the appropriate factor. Notice that if all seven factors' (i.e.,  and the six
and the six 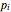 's) minimum and maximum values are the same, the program will render the conventional Fermi solution plotted as a spike. Also, if all but one of the seven factors' minimum and maximum values are the same, then the program will generate random estimates with a uniform distribution. In that case, although the program still generates a corresponding lognormal distribution curve, it may no longer be representative.
's) minimum and maximum values are the same, the program will render the conventional Fermi solution plotted as a spike. Also, if all but one of the seven factors' minimum and maximum values are the same, then the program will generate random estimates with a uniform distribution. In that case, although the program still generates a corresponding lognormal distribution curve, it may no longer be representative.
The difference between this Demonstration and the Demonstration Expanded Fermi Solution for Risk Assessment is that the initial number estimates are calculated by dividing the entered  's by the product of the corresponding six
's by the product of the corresponding six 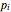 's.
's.
References:
H. C. von Baeyer, The Fermi Solution: Reflections on the Meaning of Physics, London: Penguin, 1993.
M. Peleg, M. D. Normand, J. Horowitz, and M. G. Corradini, "An Expanded Fermi Solution for Microbial Risk Assessment," International Journal of Food Microbiology, 113(1), 2007 pp. 92–101.
Permanent Citation