Extracting Microbial Inactivation Parameters from Final Survival Ratios

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Recording truly isothermal microbial survival curves, especially at high lethal temperatures, is extremely difficult if not impossible. When a microbe’s thermal inactivation kinetics is known to follow a three-parameter model, the three parameters can be estimated directly from the final survival ratios after three dynamic heat treatments, which also eliminates the need to determine the entire survival curves. The method is demonstrated with simulated non-isothermal survival data of two bacterial vegetative cells and two bacterial endospores using the Weibull log-logistic (WeLL) model with a constant shape factor.
[more]
Contributed by: Mark D. Normand and Micha Peleg (May 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
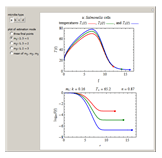
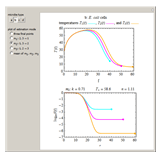
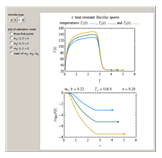
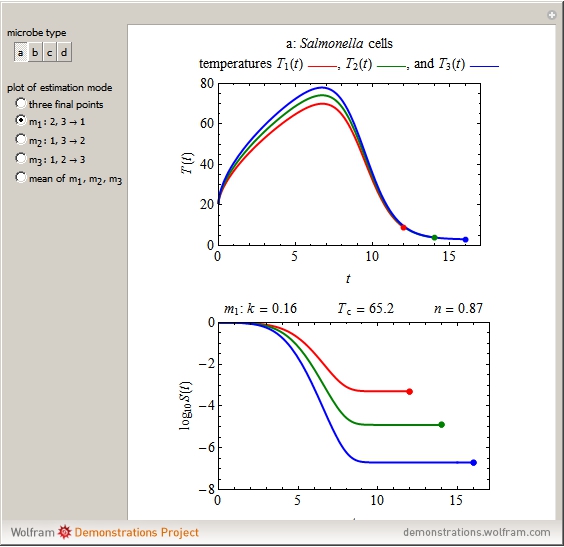
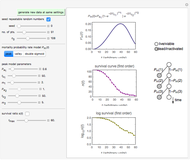
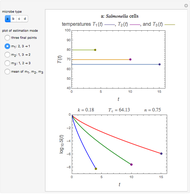
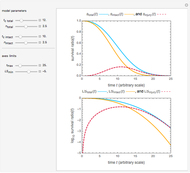
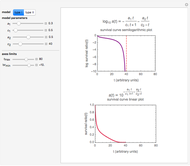
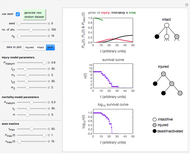
The snapshots show the three-points method applied to simulated dynamic inactivation of:
Snapshot 1: Salmonella-like vegetative cells
Snapshot 2: E. coli-like vegetative cells
Snapshot 3: Bacillus-like endospores by an Ultra High Temperature (UHT) process
Snapshot 4: Clostridium-like endospores in a conventional heat-sterilization process
Microbial thermal inactivation parameters have been traditionally determined from survival curves recorded at several constant temperatures. This method is only applicable to temperatures where the come-up and cooling times are negligible. It also requires the recording of the entire survival curves, which might be inconvenient and costly. It has been demonstrated [1, 2, 3] that if the inactivation kinetics is known to follow a particular three-parameter model, this model's parameters can be determined directly from the final survival ratios after dynamic (non-isothermal) heat treatments, without recording any intermediate survival ratios.
This Demonstration illustrates the principle with simulated non-isothermal inactivation data of Salmonella and E. coli-type vegetative cells and of heat-resistant Bacillus and Clostridium endospores; choose one by clicking "a", "b", "c", or "d", respectively, in the setter bar. Their isothermal heat inactivation is described by the three-parameter Weibull log-logistic (WeLL) model [4]: 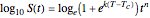 , where
, where 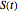 is the momentary survival ratio at time
is the momentary survival ratio at time  in minutes, that is,
in minutes, that is, 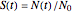 , where
, where 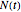 and
and 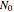 are the momentary and initial numbers, respectively,
are the momentary and initial numbers, respectively, 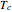 marks the inactivation onset temperature,
marks the inactivation onset temperature,  is the slope of the rate parameter at
is the slope of the rate parameter at 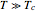 , and
, and  is the Weibullian distribution's shape factor. (Where
is the Weibullian distribution's shape factor. (Where 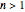 , the isothermal survival curve is concave down and where
, the isothermal survival curve is concave down and where 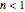 , it is concave up ("tailing"). What is known as "first-order inactivation kinetics" is a special case of the Weibullian model where
, it is concave up ("tailing"). What is known as "first-order inactivation kinetics" is a special case of the Weibullian model where  .) Ideally, after three non-isothermal heat treatments of durations
.) Ideally, after three non-isothermal heat treatments of durations 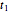 ,
, 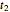 , and
, and  , with temperature profiles
, with temperature profiles  ,
, 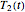 , and
, and 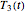 , the corresponding final survival ratios are
, the corresponding final survival ratios are 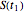 ,
, 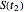 , and
, and  , and their logarithms are
, and their logarithms are 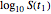 ,
, 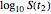 , and
, and 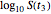 . These are the solutions of the differential equation [4]
. These are the solutions of the differential equation [4]  , where
, where 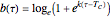 and
and  , for the three temperature profiles
, for the three temperature profiles  ,
, 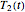 , and
, and 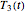 . From the three solutions for
. From the three solutions for 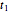 ,
, 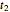 , and
, and  , the three unknown survival parameters
, the three unknown survival parameters  ,
, 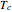 , and
, and  , in the particular medium, can be extracted using the built-in Mathematica function FindRoot [1, 2].
, in the particular medium, can be extracted using the built-in Mathematica function FindRoot [1, 2].
The WeLL model's three survival parameters,  ,
, 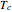 , and
, and  , are calculated in the Demonstration and displayed above the graph depicting the corresponding recreated survival curves. Because the solution of the three nonlinear simultaneous equations, which themselves are the numerical solutions of three differential equations, is sensitive to even minute experimental scatter in the final survival ratios, we have adapted an iterative procedure where the parameter
, are calculated in the Demonstration and displayed above the graph depicting the corresponding recreated survival curves. Because the solution of the three nonlinear simultaneous equations, which themselves are the numerical solutions of three differential equations, is sensitive to even minute experimental scatter in the final survival ratios, we have adapted an iterative procedure where the parameter  rises incrementally from a small value (or can fall decrementally from a high value). For each new value of
rises incrementally from a small value (or can fall decrementally from a high value). For each new value of  , two equations, those for
, two equations, those for  and
and 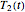 for example, are solved to extract the corresponding values of
for example, are solved to extract the corresponding values of 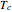 and
and  . These in turn are used to calculate the final survival ratio for the third temperature profile,
. These in turn are used to calculate the final survival ratio for the third temperature profile, 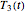 in this case, and compare it with the actual value of
in this case, and compare it with the actual value of 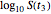 . Once the difference is smaller than the chosen tolerance (0.001 to 0.01 in this Demonstration), the corresponding values of
. Once the difference is smaller than the chosen tolerance (0.001 to 0.01 in this Demonstration), the corresponding values of  ,
, 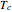 , and
, and  are considered the sought survival parameters [1, 2]. The procedure can be repeated by solving the equations of the final survival ratios at
are considered the sought survival parameters [1, 2]. The procedure can be repeated by solving the equations of the final survival ratios at 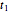 and
and  and testing the solutions against the final survival ratio
and testing the solutions against the final survival ratio 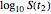 . A third alternative is to solve the equations for the final survival ratios at
. A third alternative is to solve the equations for the final survival ratios at 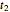 and
and  and test the solution against the final survival ratio
and test the solution against the final survival ratio 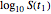 . Averaging the parameter values obtained in these three combinations is also an option, chosen with the last radio button. (To increase the results' reliability, one should use the procedure with the final survival ratios obtained under four or more temperature profiles, which will dramatically increase the number of combinations and allow the identification of outliers by statistical criteria [1, 2, 3].)
. Averaging the parameter values obtained in these three combinations is also an option, chosen with the last radio button. (To increase the results' reliability, one should use the procedure with the final survival ratios obtained under four or more temperature profiles, which will dramatically increase the number of combinations and allow the identification of outliers by statistical criteria [1, 2, 3].)
Notice that the Demonstration is only intended to illustrate the principle and method. In its actual use, the model ought to be confirmed and the solutions verified by predicting the final survival ratios after treatments having temperature profiles not used in the calculation of the three survival parameters.
In principle, the method described in this Demonstration can also be used for non-thermal antimicrobial treatments, such as disinfection with a dissipating chemical agent, in which case the concentration profile 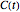 will replace the temperature profile
will replace the temperature profile 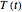 , and
, and 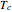 would be replaced by
would be replaced by 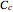 in the WeLL model.
in the WeLL model.
References
[1] M. Peleg, M. D. Normand, M. G. Corradini, A. J. van Asselt, P. de Jong, and P. F. ter Steeg, "Estimating the Heat Resistance Parameters of Bacterial Spores from Their Survival Ratios at the End of UHT and Other Heat Treatments," Critical Reviews in Food Science and Nutrition, 48(7), 2008 pp. 634–648. www.tandfonline.com/doi/abs/10.1080/10408390701724371#.UaUMT5y8N1E.
[2] M. G. Corradini, M. D. Normand, and M. Peleg, "Prediction of an Organism's Inactivation Patterns from Three Single Survival Ratios Determined at the End of Three Non-Isothermal Heat Treatments," International Journal of Food Microbiology, 126(1–2), 2008 pp. 98–111. www.sciencedirect.com/science/article/pii/S0168160508002420.
[3] M. G. Corradini, M. D. Normand, C. Newcomer, D. W. Schaffner, and M. Peleg, "Extracting Survival Parameters from Isothermal, Isobaric and 'Iso-concentration' Inactivation Experiments by the '3 End Points Method'," Journal of Food Science 74(3), 2009 pp. R1–R11. onlinelibrary.wiley.com/doi/10.1111/j.1750-3841.2008.00980.x/full.
[4] M. Peleg, Advanced Quantitative Microbiology for Food and Biosystems: Models for Predicting Growth and Inactivation, Boca Raton, FL: CRC Press, 2006.
Permanent Citation