Microbial Population Growth, Mortality, and Transitions between Them

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
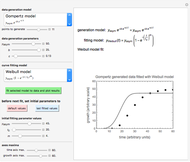
This Demonstration simulates different patterns in the evolution of microbial populations. It can describe unlimited growth, growth reaching equilibrium, growth ending in mortality, pure mortality, and mortality ending in new growth. It is based on a deterministic version of a probabilistic model originally developed for microbial cell growth, where a member of the population, after any time increment, can be in one of three states: alive but undivided, divided, or dead, with probability rates that vary with time.
Contributed by: Mark D. Normand and Micha Peleg (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
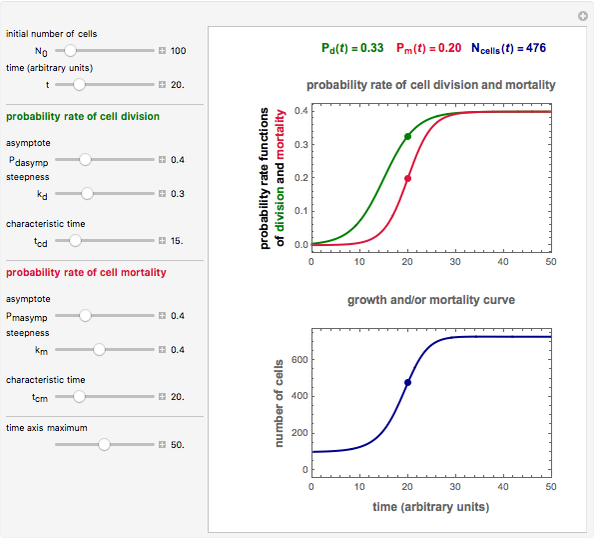
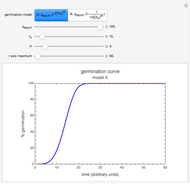
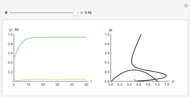
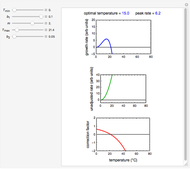
Snapshot 1: logistic ("sigmoid") growth
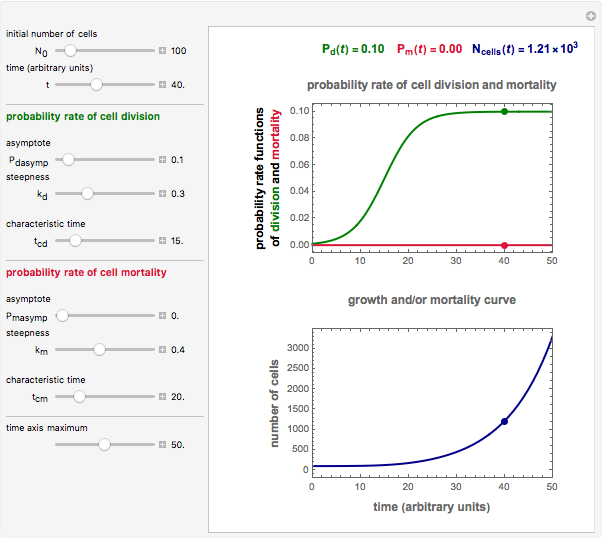
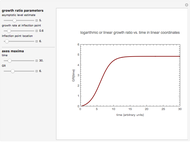
Snapshot 2: exponential growth
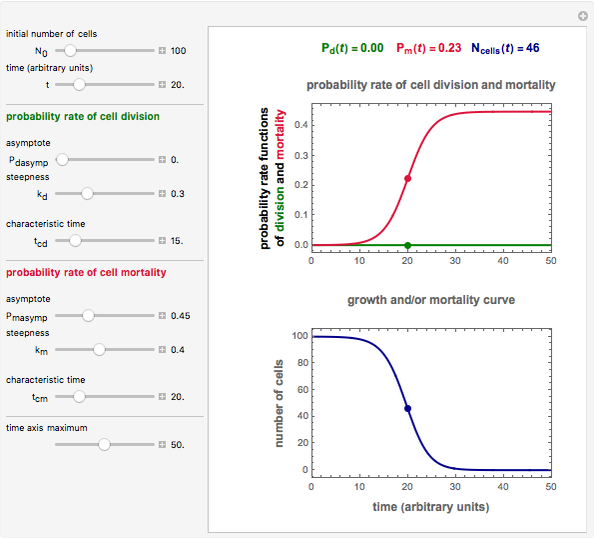
Snapshot 3: pure mortality
Snapshot 4: mortality followed by renewed growth
This Demonstration describes the evolution of a microbial population. A viable cell at time  can be in one of three states at time
can be in one of three states at time  : divided with a probability of
: divided with a probability of  , dead with a probability of
, dead with a probability of  , or alive but undivided with a probability of
, or alive but undivided with a probability of  , where
, where  and
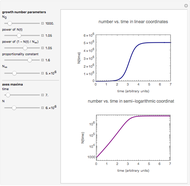
and  are the division and mortality probability rate functions, respectively. These two functions are assumed to be logistic, that is, governed by three parameters each:
are the division and mortality probability rate functions, respectively. These two functions are assumed to be logistic, that is, governed by three parameters each:  or
or  ,
, 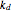 or
or  , and
, and  or
or  , all of which have their values entered with sliders. They represent these probability rate functions' asymptotic level, rate of ascent, and the time location of the inflection point, respectively, that is,
, all of which have their values entered with sliders. They represent these probability rate functions' asymptotic level, rate of ascent, and the time location of the inflection point, respectively, that is,  and
and  . The Demonstration then calculates and plots the number of cells alive at time
. The Demonstration then calculates and plots the number of cells alive at time  ,
,  , descendent of the specified initial number,
, descendent of the specified initial number,  . The calculation is based on a version of the model for the limiting case where
. The calculation is based on a version of the model for the limiting case where  tends to zero, making it continuous and fully deterministic.
tends to zero, making it continuous and fully deterministic.
You can modify the probability rate functions to create curves depicting growth, mortality, and transitions between them. You can also enter the initial number of cells,  , to calculate the number of cells at a chosen time
, to calculate the number of cells at a chosen time  ,
,  , and you can set the maximum value of the time axis in the plots. The top plot in the panel shows the chosen
, and you can set the maximum value of the time axis in the plots. The top plot in the panel shows the chosen  and
and  functions and the bottom plot shows the corresponding growth and/or mortality curve,
functions and the bottom plot shows the corresponding growth and/or mortality curve,  .
.
References:
J. Horowitz, M. D. Normand, M. G. Corradini, and M. Peleg, "Probabilistic Model of Microbial Cell Growth, Division and Mortality," Applied and Environmental Microbiology, 76(1), 2010 pp. 230–242.
M. G. Corradini, M. D. Normand, and M. Peleg, "A Stochastic and Deterministic Model of Microbial Heat Inactivation," Journal of Food Science, 75, 2010 pp. R59–R70.
Permanent Citation