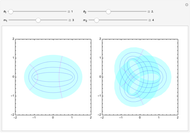
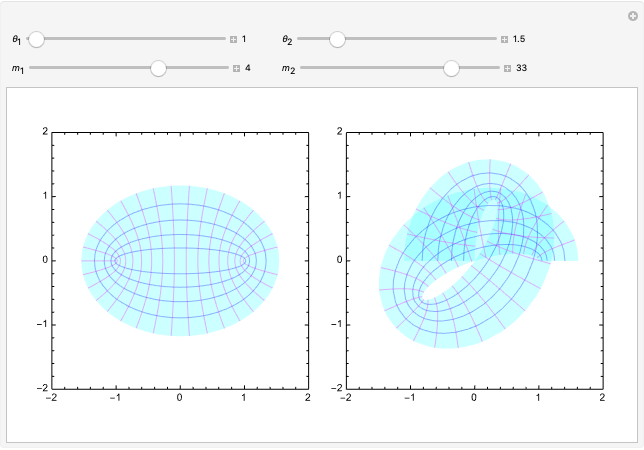
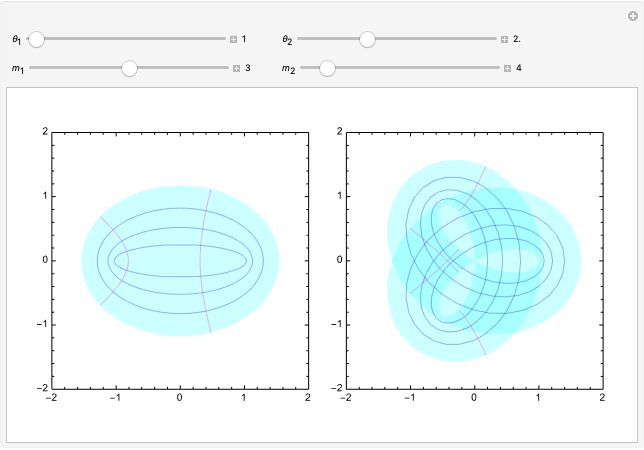
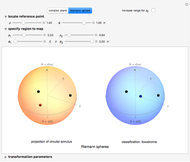
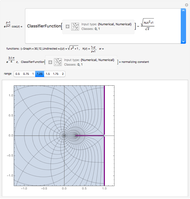
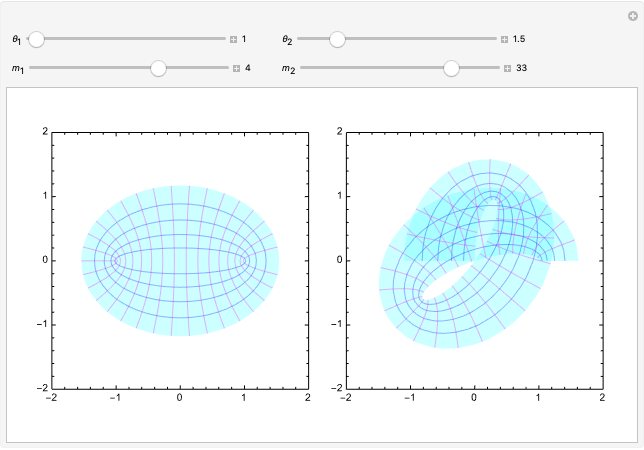
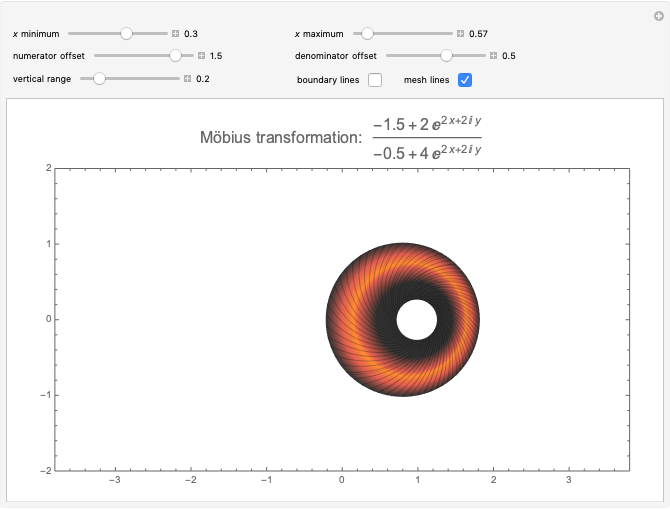
This Demonstration illustrates deformations of the plot of 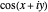in the complex plane. The real and imaginary contours of the cosine form a conformal grid and are locally homeomorphic to the two-dimensional Euclidean grid. The magenta contours show linearly spaced values of the real variable , a family of hyperbolas. The blue contours show confocal ellipses corresponding to linearly spaced values of . The left panel plots the contours of the cosine function, while the right panel plots 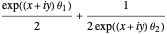, which is an adaptation of Euler's formula. With distinct values of 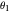and 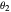, you can create hinge-like folds at the focal points. 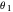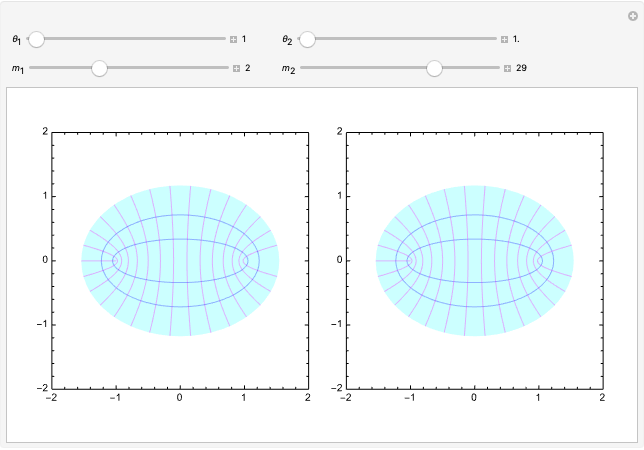If the coefficients and 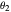are equal with integers 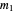and 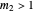, the folding process yields multiple perfectly aligned sheets.