Möbius Transformations on the Complex Plane and Riemann Sphere

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Mappings by a Möbius (or bilinear) transformation are considered on both the complex plane and the Riemann sphere. A reference point and adjustable grid are specified in polar coordinates, and the mapping can be varied using eight real parameters specifying a Möbius transformation. Bookmarks can be used to save parameters illustrating some interesting properties of the transformation.
Contributed by: Richard L. Fearn (January 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
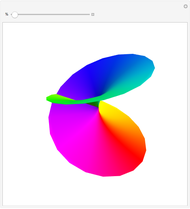
This Demonstration shows the mapping of a specified point and an associated mesh from the complex 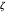 plane to the complex
plane to the complex  plane using the Möbius transformation
plane using the Möbius transformation
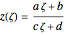 ,
,
where  ,
,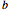 ,
,  and
and  are complex numbers. For the special case
are complex numbers. For the special case 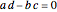 , every point in the
, every point in the 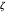 plane maps to the same image point
plane maps to the same image point 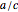 in the
in the  plane, thus crushing the plane to a point. This case can be excluded by requiring that
plane, thus crushing the plane to a point. This case can be excluded by requiring that 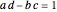 , giving the so-called normal form. The normal form of the Möbius transformation is used to classify transformations as parabolic, elliptic, hyperbolic or loxodromic.
, giving the so-called normal form. The normal form of the Möbius transformation is used to classify transformations as parabolic, elliptic, hyperbolic or loxodromic.
A fixed point of a Möbius transformation occurs at points when the transformation maps a point 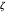 to itself,
to itself, 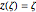 . Except for the uninteresting case mentioned above and the identity transformation (where every point is a fixed point), there are always two fixed points, which may coalesce.
. Except for the uninteresting case mentioned above and the identity transformation (where every point is a fixed point), there are always two fixed points, which may coalesce.
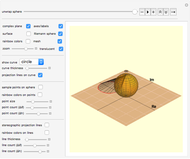
Complex numbers can be represented as points in a plane or on a Riemann sphere, produced by a stereographic projection 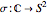 , where
, where 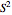 is a sphere. Including the point at infinity is necessary to define the extended complex plane, but this point occurs naturally on the Riemann sphere as the north pole.
is a sphere. Including the point at infinity is necessary to define the extended complex plane, but this point occurs naturally on the Riemann sphere as the north pole.
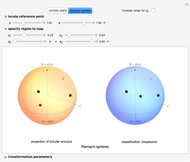
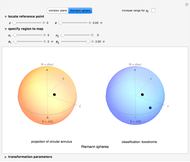
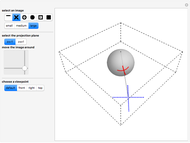
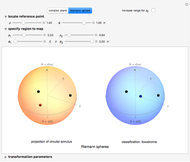
Buttons allow you to choose the mapping on the complex plane or on the Riemann sphere. Use the "increase range for 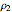 " checkbox to extend the range of the plotted mesh. The "locate reference point" sliders control the location of a reference point in polar coordinates. The hidden "specify region to map" sliders control a mesh in polar coordinates centered at the reference point. The "transformation parameters" sliders hidden below the graphics control eight real parameters specifying a Möbius transformation.
" checkbox to extend the range of the plotted mesh. The "locate reference point" sliders control the location of a reference point in polar coordinates. The hidden "specify region to map" sliders control a mesh in polar coordinates centered at the reference point. The "transformation parameters" sliders hidden below the graphics control eight real parameters specifying a Möbius transformation.
Controls are initially set to clarify the overall presentation of results on the Riemann sphere. North and south poles locate the points at 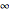 and
and  , and the equator corresponds to the unit circle. Toggle between the Riemann sphere and the complex plane to see different representations of the same information. Also shown are the coordinate systems
, and the equator corresponds to the unit circle. Toggle between the Riemann sphere and the complex plane to see different representations of the same information. Also shown are the coordinate systems 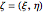 , in which a reference point and its associated grid are specified (left illustration), and
, in which a reference point and its associated grid are specified (left illustration), and 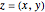 , showing the image under a Möbius transformation (right illustration). The reference point and mesh marking the specified region and their images are color coded. Also shown in black are the fixed points of the transformation. The classification of the transformation is given in a label below the right illustration.
, showing the image under a Möbius transformation (right illustration). The reference point and mesh marking the specified region and their images are color coded. Also shown in black are the fixed points of the transformation. The classification of the transformation is given in a label below the right illustration.
Fixed points: Snapshot 1 suppresses the mesh and its image to emphasize the locations of the points of interest on the Riemann sphere. The point specified is shown in red and the image point is shown in blue; coalesced fixed points are shown in black. Open the controls for the transformation parameters, select any parameter and change its value; the fixed points should separate and move.
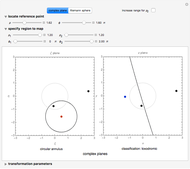
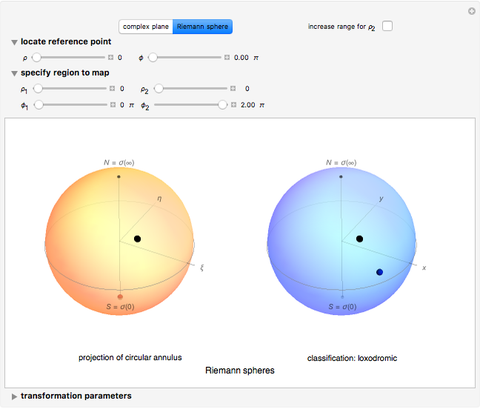
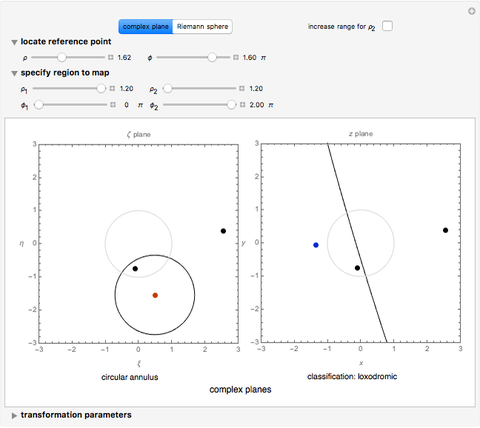
Circles: Snapshot 2 illustrates a property of the Möbius transformation: that circles map to circles. Parameters are initially set to describe a thin annulus that approximates a circle. The initial position of the reference point is set so that the line in the  plane appears to be straight. To clarify this, switch to the Riemann sphere and note that an obvious circle passes through the north pole (point at infinity). A straight line in the complex plane is a circle of infinite radius. There are some combinations of parameters for which the circles are not resolved computationally in a complex plane, but this could be achieved by increasing the computational time. Circles of different sizes require coordinating changes in the controls specifying the radii
plane appears to be straight. To clarify this, switch to the Riemann sphere and note that an obvious circle passes through the north pole (point at infinity). A straight line in the complex plane is a circle of infinite radius. There are some combinations of parameters for which the circles are not resolved computationally in a complex plane, but this could be achieved by increasing the computational time. Circles of different sizes require coordinating changes in the controls specifying the radii 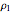 ,
, 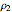 of the annulus. Change the location of the reference point or any of the transformation parameters to specify different circles and different Möbius transformations. Toggle back and forth between the complex plane and the Riemann sphere as desired.
of the annulus. Change the location of the reference point or any of the transformation parameters to specify different circles and different Möbius transformations. Toggle back and forth between the complex plane and the Riemann sphere as desired.
Regions: Snapshot 3 illustrates that the mesh lines in the specified annulus and its image intersect locally at right angles. This indicates that the mapping is either conformal or anticonformal. To choose between the two possibilities, you could check algebraically if the Cauchy–Riemann conditions are satisfied by the function describing the Möbius transformation (they are), but there is also a visual check. Notice that the specified region in the 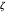 plane is the region between two concentric circles centered at the specified reference point, and that the image region is also a region between two circles. For conformal mapping, the region to the left of a circle maps to the region to the left of the image circle. Open the controls for the region to map and wiggle the control for
plane is the region between two concentric circles centered at the specified reference point, and that the image region is also a region between two circles. For conformal mapping, the region to the left of a circle maps to the region to the left of the image circle. Open the controls for the region to map and wiggle the control for 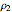 slightly to identify the image of the outer circle of the annulus. Then increase
slightly to identify the image of the outer circle of the annulus. Then increase 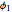 to see that the region to the left of the outer circle in the
to see that the region to the left of the outer circle in the 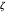 plane maps to the region to the left of the corresponding image circle.
plane maps to the region to the left of the corresponding image circle.
An interesting characteristic of Wolfram Mathematica shows up. Mathematica sometimes shades the region outside the region described by ParametricPlot. As you increase 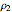 , the radius of the outer circle increases until it becomes a circle of infinite radius (straight line). Additionally increasing
, the radius of the outer circle increases until it becomes a circle of infinite radius (straight line). Additionally increasing 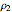 changes the shading of the region that is not meshed, from white to light blue. Switch to the Riemann sphere for a simple visualization of what happened. When the point at infinity is within the meshed region, ParametricPlot changes shading outside of the region from white to light blue.
changes the shading of the region that is not meshed, from white to light blue. Switch to the Riemann sphere for a simple visualization of what happened. When the point at infinity is within the meshed region, ParametricPlot changes shading outside of the region from white to light blue.
Complex inversion: Snapshot 4 shows the mapping properties of complex inversion, which also can be thought of as two successive reflections: one in the unit circle and one in the real axis. The composition of two reflections constitutes a conformal mapping. Note that the example starts with the specified reference point being the origin and the region being interior to the unit circle. Fixed points are located at 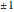 . Switch to the Riemann sphere and note that the region inside the unit circle corresponds to the southern hemisphere, and the image region corresponds to the northern hemisphere. This view also shows clearly that the image point is at
. Switch to the Riemann sphere and note that the region inside the unit circle corresponds to the southern hemisphere, and the image region corresponds to the northern hemisphere. This view also shows clearly that the image point is at  .
.
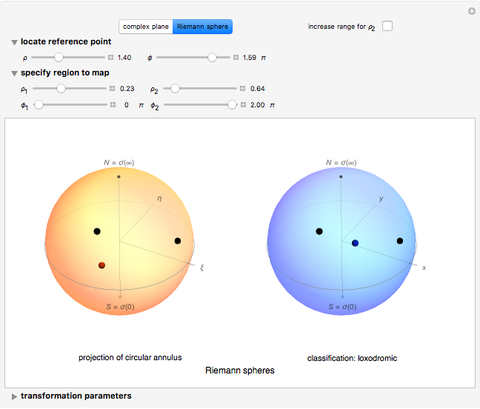
Classification: Snapshot 5 illustrates the classification of Möbius transformations by the following criterion in normal form: parabolic, 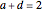 ; elliptic,
; elliptic, 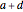 is real and
is real and 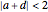 ; hyperbolic,
; hyperbolic, 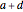 is real and
is real and 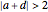 ; loxodromic,
; loxodromic, 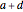 is complex. Translation is an example of a parabolic transformation; show the animation controls and play or increment the controls for
is complex. Translation is an example of a parabolic transformation; show the animation controls and play or increment the controls for 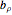 and/or
and/or 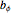 . Return to the "classification" bookmark and play the control for
. Return to the "classification" bookmark and play the control for 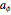 ; this gives a clear visualization of rotation and is an example of an elliptic transformation. Return
; this gives a clear visualization of rotation and is an example of an elliptic transformation. Return 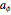 to zero, and play
to zero, and play 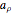 ; this is scaling and is an example of a hyperbolic transformation. Playing
; this is scaling and is an example of a hyperbolic transformation. Playing 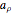 and
and 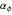 simultaneously is a transformation for rotation and scaling, which is an example of a loxodromic transformation. You may need to change the play speed or step the controls to see the motions clearly.
simultaneously is a transformation for rotation and scaling, which is an example of a loxodromic transformation. You may need to change the play speed or step the controls to see the motions clearly.
Unit Disk: Snapshot 6 shows a Möbius transformation that maps a unit disk to the upper half-plane. Notice that a circle of infinite radius describes the straight line corresponding to the real axis in the  plane. Switch to the Riemann sphere to see that the real axis is projected to a great circle passing through the north pole.
plane. Switch to the Riemann sphere to see that the real axis is projected to a great circle passing through the north pole.
Reference
[1] T. Needham, Visual Complex Analysis, New York: Oxford University Press, 1997.
Permanent Citation