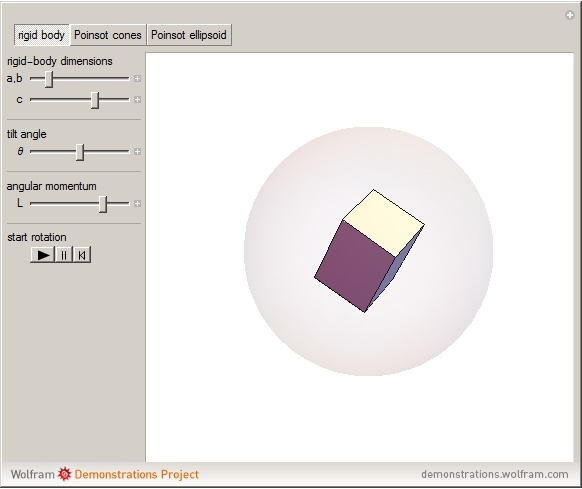
Free Rotation of a Rigid Body: Poinsot Constructions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The torque-free rotation of a rigid body can be described by Euler's three equations of motion:  , and cyclic permutations, where
, and cyclic permutations, where  ,
,  ,
,  are the principal moments of inertia and
are the principal moments of inertia and  ,
,  ,
,  are the angular velocities around their respective principal axes in the fixed-body coordinate system. There are two constants of the motion, the angular momentum
are the angular velocities around their respective principal axes in the fixed-body coordinate system. There are two constants of the motion, the angular momentum  and the kinetic energy
and the kinetic energy  . Euler's equations can be solved in closed form, giving
. Euler's equations can be solved in closed form, giving  ,
,  ,
,  in terms of Jacobi elliptic integrals.
in terms of Jacobi elliptic integrals.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
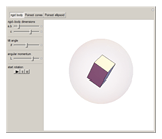
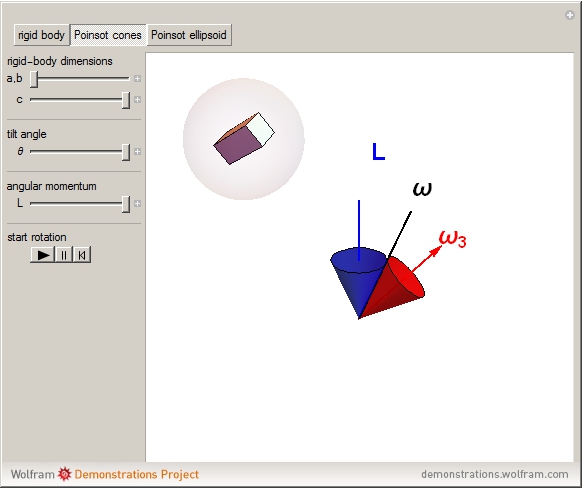
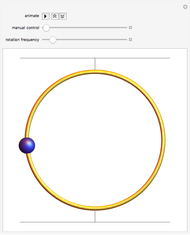
Snapshot 1: cuboid rigid body
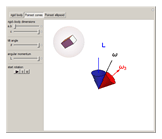
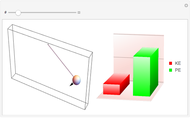
Snapshot 2: cone construction for prolate rotor ( )
)
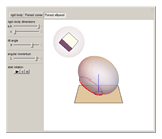
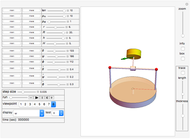
Snapshot 3: Poinsot construction for oblate rotor ( )
)
References:
H. Goldstein, Classical Mechanics, Cambridge, MA: Addison–Wesley, 1950 pp. 156–163.
J. L. Synge and B. A. Griffiths, Principles of Mechanics, 2nd ed., New York: McGraw–Hill, 1949 pp. 418–429.
Permanent Citation