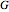Frequency-Modulated Continuous-Wave (FMCW) Radar

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
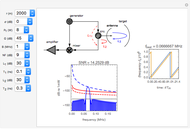
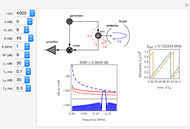
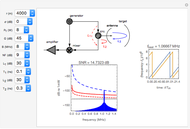
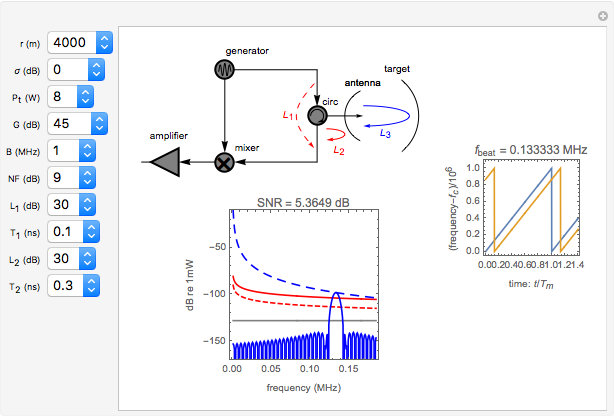
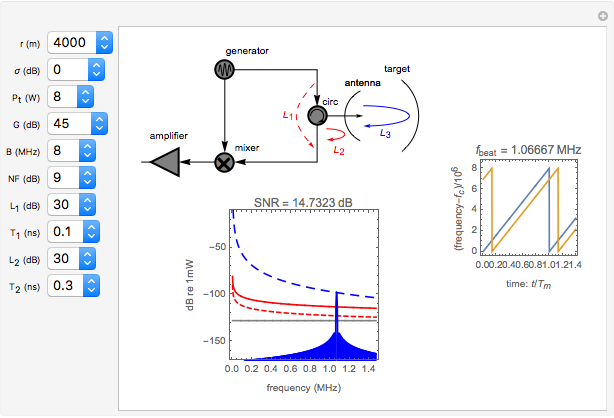
Ordinary pulsed radar detects the range to a target by emitting a short pulse and observing the time of flight of the target echo. This requires the radar to have high instantaneous transmit power and often results in a radar with a large, expensive physical apparatus. Frequency-modulated continuous-wave (FMCW) radars achieve similar results using much smaller instantaneous transmit powers and physical size by continuously emitting periodic pulses whose frequency content varies with time. A very important type of FMCW radar pulse is the linear FM sweep. In this case, the range to the target is found by detecting the frequency difference between the received and emitted radar signals. The range to the target is proportional to this frequency difference, which is also referred to as the beat frequency.
[more]
Contributed by: Marshall Bradley (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In a frequency-modulated continuous-wave (FMCW) radar employing a linear upsweep in frequency, the radar signal generator produces a phase modulated signal of the form
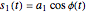 ,
,
where
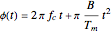
is the signal phase at time  ,
, 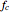 is the radar carrier frequency,
is the radar carrier frequency, 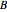 is the sweep width, and
is the sweep width, and 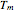 is the pulse repetition period. The instantaneous frequency of the transmitted signal is
is the pulse repetition period. The instantaneous frequency of the transmitted signal is
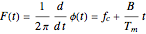 .
.
In the course of the time interval  the radar frequency linearly varies between
the radar frequency linearly varies between 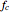 and
and  .
.
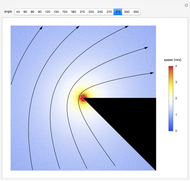
In FMCW radar, the signal generated by the radar is split into two parts. A small portion is allowed to pass into the upper port of the radar mixer where it is used as a reference signal for detection of the echo signal. The other, larger portion of the generated signal passes out through the circulator and into the antenna. The circulator is a multiport, electronic device that only allows electrical signals to propagate in the clockwise direction. Use of a circulator allows the radar to share transmit and receive antennas. After exiting the antenna, this signal propagates into the air out to a target where it is reflected and returns to the antenna. It then goes back into the circulator, passes through in the preferred direction and into the horizontal port of the mixer. If the target is located at distance  from the radar, then the echo signal that comes into the mixer can be written in the form
from the radar, then the echo signal that comes into the mixer can be written in the form
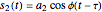 ,
,
where 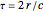 is the propagation delay of the echo,
is the propagation delay of the echo,  is the speed of light, and
is the speed of light, and 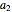 is a factor that accounts for propagation losses, target reflectivity, and a variety of radar performance parameters.
is a factor that accounts for propagation losses, target reflectivity, and a variety of radar performance parameters.
The mixer multiplies the echo signal and the reference signal that came into the upper port of the mixer. This process produces sum and difference frequencies. The sum frequencies are on the order of twice the radar carrier frequency. The radar electronic circuits cannot respond to signals at this frequency. Thus only the difference frequencies pass out of the mixer. The signal that comes out of the mixer can be written
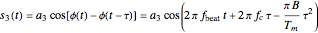 ,
,
where
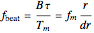
is the beat frequency of the target echo, 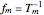 is the radar pulse modulation frequency, and
is the radar pulse modulation frequency, and 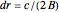 is the range resolution of the radar pulse.
is the range resolution of the radar pulse.
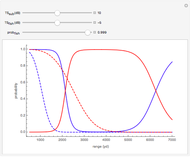
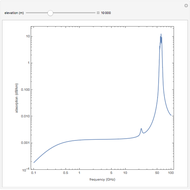
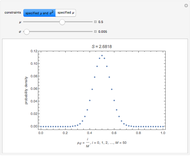
In FMCW radar applications, targets are found by performing Fourier analysis on the mixer output signal. Using a Fourier transform with a rectangular window of integration extending over a time interval of length 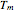 leads to the following representation of the power in the mixer output signal:
leads to the following representation of the power in the mixer output signal:
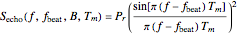 .
.
Here 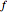 is the analysis frequency and
is the analysis frequency and 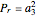 is the power of the target echo. In terms of the standard radar equation, the target echo power
is the power of the target echo. In terms of the standard radar equation, the target echo power 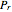 can be written
can be written
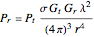 ,
,
where  is the radar transmission power (W),
is the radar transmission power (W),  is the radar cross section
is the radar cross section 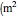 ),
), 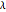 is the wavelength of the radar (m),
is the wavelength of the radar (m),  is the distance from the radar to the target (m), and
is the distance from the radar to the target (m), and 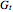 and
and  are the gains on a power scale of the transmit and receive antennas. For a single antenna system these gains are equal (
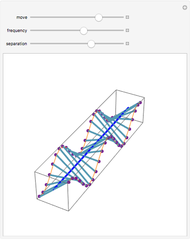
are the gains on a power scale of the transmit and receive antennas. For a single antenna system these gains are equal ( ). Gain is usually expressed on a decibel scale. The target echo path is illustrated by the solid blue line
). Gain is usually expressed on a decibel scale. The target echo path is illustrated by the solid blue line  in the circuit diagram.
in the circuit diagram.
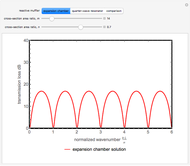
It is more effective to perform the Fourier analysis of the mixer output signal with a nonuniform window of integration in order to reduce side lobes in the spectral response. For the case of a Hamming window of integration
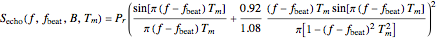 .
.
Use of the Hamming window of integration allows the detection of targets that are close together in range with large differences in echo level. Otherwise the 13 dB down side lobes (rectangular window) from the target with the larger echo will obscure the return from the target with the weaker echo.
The detection performance of the radar is limited by phase noise that propagates via the parasitic paths 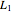 and
and 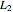 illustrated as the dashed and solid red lines in the circuit diagram. The power spectrum of the phase noise of the signal generator is modeled via
illustrated as the dashed and solid red lines in the circuit diagram. The power spectrum of the phase noise of the signal generator is modeled via
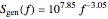 .
.
It is measured in units of W/Hz. If the phase noise effects are included in the representation for the FMCW beat signal out of the mixer, then
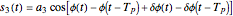 ,
,
where  is the phase of the phase noise at time
is the phase of the phase noise at time  and
and 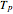 is the difference in travel time on the parasitic path (
is the difference in travel time on the parasitic path (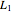 or
or 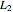 ) and the travel time on the reference path that goes directly from the signal generator to the mixer. If the parasitic path and the reference path have the same travel times then the phase noise cancels.
) and the travel time on the reference path that goes directly from the signal generator to the mixer. If the parasitic path and the reference path have the same travel times then the phase noise cancels.
The frequency transfer function that models the process of obtaining a difference between two noise processes where one is a time-delayed version of the other is
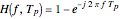 .
.
The phase noise that limits radar performance is
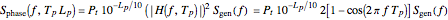 ,
,
where  is the loss in signal power measured in decibels on the parasitic path relative to the reference path.
is the loss in signal power measured in decibels on the parasitic path relative to the reference path.
Radar performance is ultimately limited by thermal noise. If 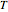 is the temperature of the radar electronics in degrees Kelvin (about 290 K at room temperature) and
is the temperature of the radar electronics in degrees Kelvin (about 290 K at room temperature) and 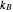 is Boltzmann's constant
is Boltzmann's constant  ), then the power spectrum of thermal noise that limits radar performance is
), then the power spectrum of thermal noise that limits radar performance is
 ,
,
where the noise factor 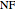 represents the decibel level increase of the radar thermal noise floor above the theoretical lower limit. An ideal (unobtainable) radar system would have a noise factor of 0 dB.
represents the decibel level increase of the radar thermal noise floor above the theoretical lower limit. An ideal (unobtainable) radar system would have a noise factor of 0 dB.
The signal-to-noise ratio for the radar echo is the ratio of signal power to the sum of all limiting noise effects. For a FMCW radar with two parasitic phase noise paths as shown, it can be written in the form
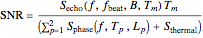 .
.
Reliable detection of a radar echo requires signal to noise ratios in excess of 10. 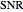 is usually expressed on a decibel scale.
is usually expressed on a decibel scale.
References
[1] G. M. Brooker, "Understanding Millimeter Wave FMCW Radars," in First International Conference on Sensing Technology, November 21–23, 2005, Palmerston North, New Zealand (G. Sen Gupta, S. C. Mukhopadhyay, and C. H. Messom, eds.), pp. 152–157.
[2] I. V. Komarov and S. M. Smolskiy, Fundamentals of Short-Range FM Radar, Boston: Artech House, 2003.
Permanent Citation