Fluid Flow around a Corner

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
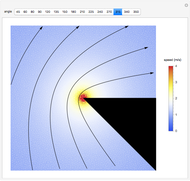
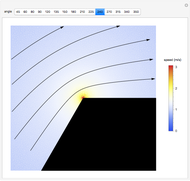
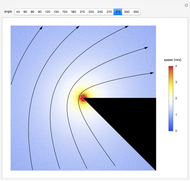
This Demonstration illustrates the effect that corners in flow channels have on the two-dimensional, irrotational flow of an inviscid fluid. When the corner angle is less than 180°, a stagnation region with low flow speeds forms in the corner. When the corner angle is greater than 180°, a region of high flow velocity forms at the tip of the corner. When the corner angle is exactly 180°, the flow is parallel to the  axis and moves from left to right at a constant speed. Warm and cold colors correspond to regions of high and low fluid speeds as indicated by the legend shown to the right. The flow streamlines are indicated by black arrows and boundary regions are shown in gray.
axis and moves from left to right at a constant speed. Warm and cold colors correspond to regions of high and low fluid speeds as indicated by the legend shown to the right. The flow streamlines are indicated by black arrows and boundary regions are shown in gray.
Contributed by: Marshall Bradley (July 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The governing partial differential equations for the steady-state, two-dimensional flow of an incompressible, irrotational, inviscid fluid in planes parallel to the  -
-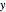 plane are the Euler equations (based on Newton's second law of motion) and the equation of continuity. The Euler equations are
plane are the Euler equations (based on Newton's second law of motion) and the equation of continuity. The Euler equations are
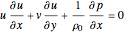 ,
,
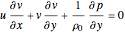 ,
,
where 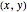 is a point in the flow field,
is a point in the flow field, 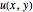 and
and 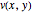 are the components of the fluid velocity vector at this point,
are the components of the fluid velocity vector at this point, 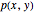 is the pressure, and
is the pressure, and 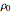 is the constant density of the fluid. The equation of continuity is
is the constant density of the fluid. The equation of continuity is
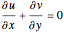 .
.
These relations provide a set of three equations for the three unknowns 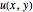 ,
, 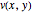 , and
, and 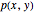 . Since the flow is assumed to be irrotational, there exists a potential function
. Since the flow is assumed to be irrotational, there exists a potential function 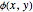 such that
such that
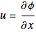 ,
, 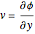 .
.
If the differential relationships  ,
, 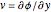 are substituted into the two Euler equations and these equations are then added together, then the resulting single equation is a perfect differential and can be integrated in closed form to yield the Bernoulli equation
are substituted into the two Euler equations and these equations are then added together, then the resulting single equation is a perfect differential and can be integrated in closed form to yield the Bernoulli equation
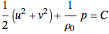 ,
,
where 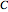 is a constant for the flow. If the differential relations between the velocities
is a constant for the flow. If the differential relations between the velocities  and
and  and the potential function
and the potential function  are substituted into the continuity equation, the result is Laplace's equation
are substituted into the continuity equation, the result is Laplace's equation
 .
.
Thus, if we can find a function 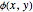 that satisfies Laplace's equation and the necessary boundary conditions, then we have a solution to the flow problem. For potential flow around corners, the boundary condition is that the normal component of the fluid velocity must be zero. This will be the case if the streamlines of the flow are always parallel to the boundaries.
that satisfies Laplace's equation and the necessary boundary conditions, then we have a solution to the flow problem. For potential flow around corners, the boundary condition is that the normal component of the fluid velocity must be zero. This will be the case if the streamlines of the flow are always parallel to the boundaries.
If 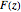 is an analytic function of the complex variable
is an analytic function of the complex variable  , then
, then 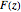 can be written in the form
can be written in the form 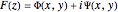 . Since
. Since 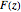 is analytic, its derivative at the point
is analytic, its derivative at the point  can be computed by approaching the point
can be computed by approaching the point  from any direction. This fact leads to the Cauchy–Riemann equations:
from any direction. This fact leads to the Cauchy–Riemann equations:
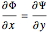 ,
, 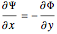 .
.
Both  and
and  satisfy Laplace's equation, so they define a two-dimensional flow field consistent with the governing equations of motion. The function
satisfy Laplace's equation, so they define a two-dimensional flow field consistent with the governing equations of motion. The function 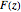 is called the complex potential and has the properties defined by the following equation:
is called the complex potential and has the properties defined by the following equation:
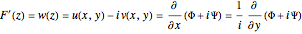 .
.
The function 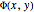 is the potential function of the flow. The gradient of
is the potential function of the flow. The gradient of 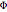 is the velocity vector
is the velocity vector 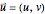 of the flow. The function
of the flow. The function 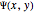 is called the stream function of the flow, and curves defined by
is called the stream function of the flow, and curves defined by 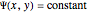 define the paths along which the fluid flows.
define the paths along which the fluid flows.
In order to model fluid flow around a corner, we choose the complex potential function 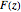 defined by the equation
defined by the equation
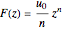 ,
,
where 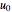 is a real-valued reference flow speed and the exponent
is a real-valued reference flow speed and the exponent  controls the magnitude of the corner angle. The relationship between
controls the magnitude of the corner angle. The relationship between  and the corner angle
and the corner angle 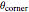 measured in degrees is
measured in degrees is
 .
.
When  , the corner angle is 180° and the fluid velocity is
, the corner angle is 180° and the fluid velocity is 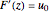 . In general, the complex fluid velocity is
. In general, the complex fluid velocity is
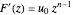 .
.
If 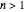 —that is, if the corner angle is less than 180°—then the fluid velocity goes to zero in the corner, thereby causing the region of stagnation. If
—that is, if the corner angle is less than 180°—then the fluid velocity goes to zero in the corner, thereby causing the region of stagnation. If 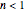 —that is, if the corner angle is greater than 180°—there is a singularity at the origin
—that is, if the corner angle is greater than 180°—there is a singularity at the origin 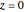 and the fluid velocity goes to infinity at this point. This is a pecell-known paradox for potential flow. In a real fluid, the effects of viscosity prevent this from happening.
and the fluid velocity goes to infinity at this point. This is a pecell-known paradox for potential flow. In a real fluid, the effects of viscosity prevent this from happening.
By beginning with a corner angle of 45° and successively increasing the corner angle up to the maximum of 350°, you can develop a feel for how the streamlines predicted by two-dimensional potential theory tend to follow the boundaries. At corner angles beyond 270°, the flow effectively reverses itself. At corner angles less than 90°, the flow effectively reaches all the way into the corner.
References
[1] G. Falkovich, Fluid Mechanics: A Short Course for Physicists, Cambridge: Cambridge University Press, 2011.
[2] G. Polya and G. Latta, Complex Variables, New York: John Wiley & Sons, 1974.
[3] L. Prandtl and O. G. Tietjens, Fundamentals of Hydro- and Aeromechanics, New York: Dover Publications, 1934.
[4] R. Snieder and K. van Wijk, A Guided Tour of Mathematical Methods for the Physical Sciences, 3rd ed., Cambridge: Cambridge University Press, 2015.
Permanent Citation