Uncertainty in Sonar Performance Prediction

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Sonar performance prediction can be viewed as a two-step process. In the first step, the statistical properties of the signal and noise fields at the sonar are estimated. The characteristic parameter is the signal to noise ratio (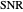 ). In the second stage,
). In the second stage, 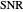 is converted to probability of detection
is converted to probability of detection 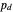 using a mapping appropriate to the sonar type and method of operation. If the
using a mapping appropriate to the sonar type and method of operation. If the  is known exactly then, the probability of detection
is known exactly then, the probability of detection 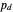 is a number on the interval
is a number on the interval 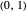 . As a practical matter
. As a practical matter 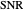 is never known with total certainty. This Demonstration illustrates the effect of uncertainty in
is never known with total certainty. This Demonstration illustrates the effect of uncertainty in 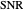 on the estimation of probability of detection
on the estimation of probability of detection  .
.
Contributed by: Marshall Bradley (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In underwater acoustics, sonar performance is predicted with the aid of the sonar equation. A simple example of a sonar equation expressed on a decibel scale applicable to passive sonar is the following: 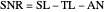 , where
, where 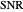 is the signal to noise ratio (dB),
is the signal to noise ratio (dB), 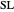 is the target source level (dB re 1 μPa at 1m),
is the target source level (dB re 1 μPa at 1m), 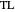 is the transmission loss (dB re 1 m), and
is the transmission loss (dB re 1 m), and  is the ambient noise level (dB re 1
is the ambient noise level (dB re 1 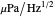 ). In practical situations the individual terms in the sonar equation are not precisely known. Thus there is uncertainty associated with an
). In practical situations the individual terms in the sonar equation are not precisely known. Thus there is uncertainty associated with an 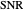 prediction.
prediction.
If we let 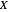 denote the
denote the 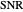 , then a plausible initial assumption is that
, then a plausible initial assumption is that 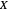 is a normally distributed random variable with probability density function
is a normally distributed random variable with probability density function
 ,
,
where 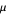 is the mean decibel
is the mean decibel  level predicted by the modeling process and
level predicted by the modeling process and 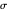 is the measure of the decibel uncertainty associated with the prediction. For example, in a situation where acoustic performance prediction models predict favorable sonar performance with high certainty, we might have
is the measure of the decibel uncertainty associated with the prediction. For example, in a situation where acoustic performance prediction models predict favorable sonar performance with high certainty, we might have 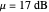 and
and 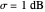 . If we let the random variable
. If we let the random variable  denote the signal to noise ratio measured on an intensity scale, then the relationship between the random variables
denote the signal to noise ratio measured on an intensity scale, then the relationship between the random variables 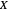 and
and 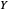 is
is
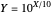
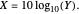
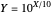 InlineMath,
InlineMath, 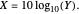 InlineMath
InlineMath
The random variable 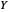 is said to have a lognormal distribution and its probability density function is
is said to have a lognormal distribution and its probability density function is
 .
.
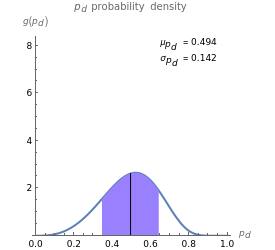
The probability density functions 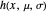 and
and 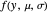 convey the same information about the uncertainty in
convey the same information about the uncertainty in 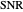 , only the scales are different. When measured on an intensity scale,
, only the scales are different. When measured on an intensity scale, 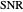 is defined on the interval
is defined on the interval  . If we measure
. If we measure 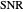 on a decibel scale, then it is defined on the interval
on a decibel scale, then it is defined on the interval 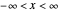 . The condition of absolutely no signal corresponds to
. The condition of absolutely no signal corresponds to 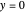 or
or 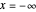 .
.  Infinite signal corresponds to infinity on both scales.
Infinite signal corresponds to infinity on both scales.
If we assume that the sonar is optimized for a signal with random phase and Rayleigh amplitude, then the appropriate mapping from  to probability of detection
to probability of detection  is ([1])
is ([1])
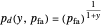 ,
,
where 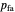 is the sonar false alarm rate and
is the sonar false alarm rate and 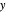 is the
is the  measured on an intensity scale. The function
measured on an intensity scale. The function 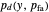 is a monotonic increasing map from intensity
is a monotonic increasing map from intensity  to probability of detection. It has the inverse function
to probability of detection. It has the inverse function
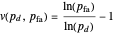 ,
,
with derivative
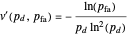 .
.
Because of the simple properties of the inverse function 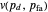 , the probability density function
, the probability density function  of probability of detection
of probability of detection  can be found in closed form. The result is
can be found in closed form. The result is
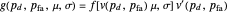 ,
,
or more completely
 ,
,  .
.
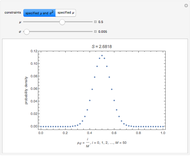
Due to the uncertainty in 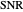 , the probability of detection
, the probability of detection 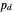 is no longer a single number but rather a statistical distribution. The expected value and variance of the probability of detection are useful characterizations of this distribution. They are defined to be
is no longer a single number but rather a statistical distribution. The expected value and variance of the probability of detection are useful characterizations of this distribution. They are defined to be
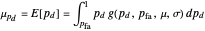 ,
,
 .
.
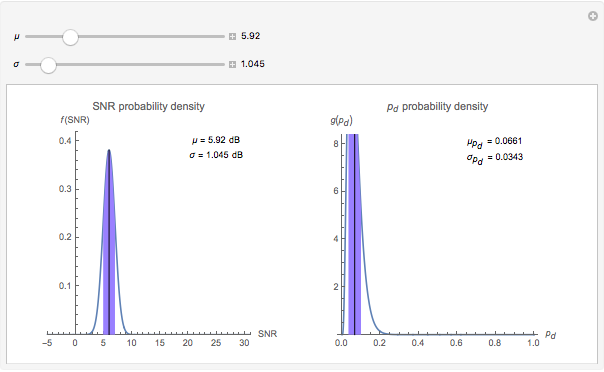
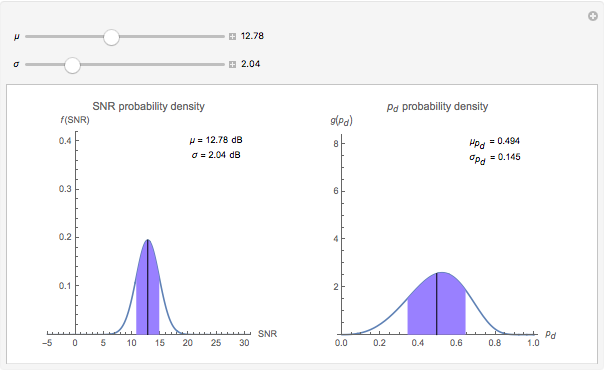
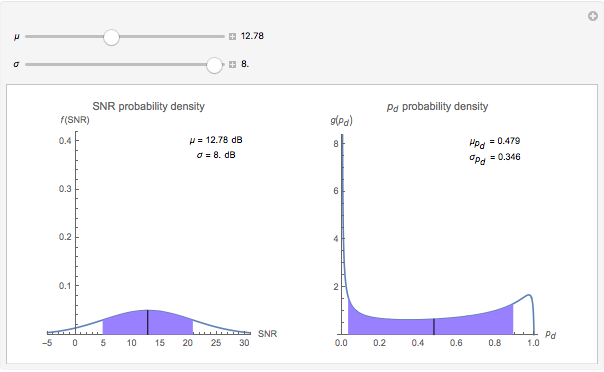
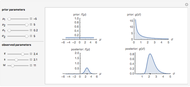
Use the two sliders to control the selection of  the mean
the mean 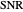 (dB) and
(dB) and 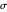 the standard deviation of
the standard deviation of 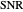 (dB). When
(dB). When 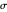 is small, the distribution of probability of detection is peaked with a relatively small standard deviation (square root of variance). This is indicative of a useful prediction of probability of detection. However, when
is small, the distribution of probability of detection is peaked with a relatively small standard deviation (square root of variance). This is indicative of a useful prediction of probability of detection. However, when  is larger, the distribution of probability of detection is much more spread out and has a much larger standard deviation. In this latter circumstance, the predicted probability of detection may not be useful due to the large associated uncertainty.
is larger, the distribution of probability of detection is much more spread out and has a much larger standard deviation. In this latter circumstance, the predicted probability of detection may not be useful due to the large associated uncertainty.
Reference
[1] A. D. Whalen, Detection of Signals in Noise, New York: Academic Press, 1971.
Permanent Citation