Risk, Ownership, and Control

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
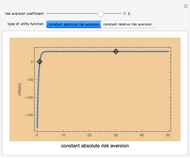
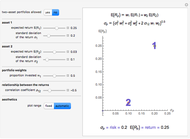
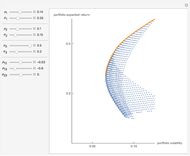
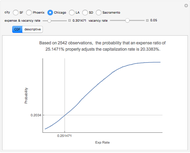
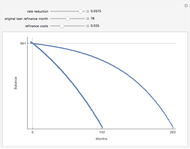
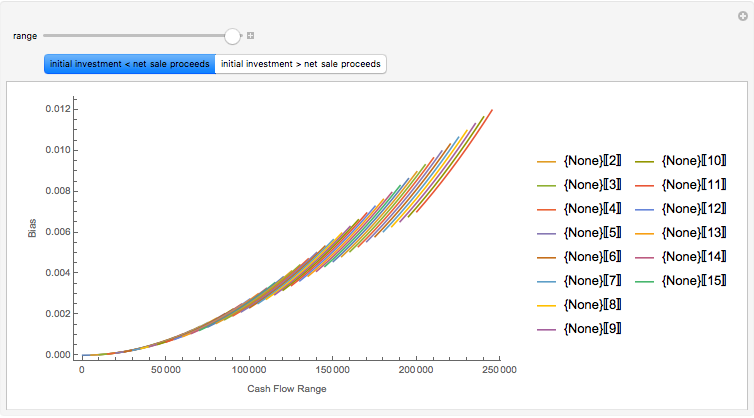
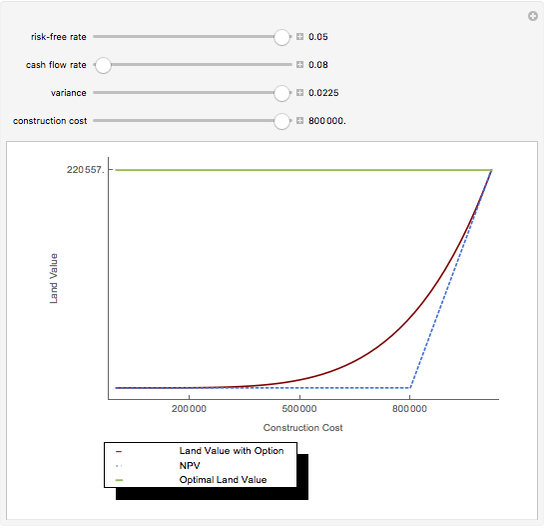
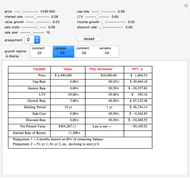
Conventional models view risk as an exogenously generated random process. Also, especially for financial assets, very often it is assumed that returns are normally distributed, an assumption that comes with considerable baggage. Recent innovations in numerically intensive methodology (made easier by Mathematica) allow modeling using non-normal heavy-tailed distributions. Another common—and realistic—assumption for financial assets is the separation of ownership and control. This Demonstration provides a way of thinking about how those assumptions might be relaxed for all investments but especially for individually owned investment real property.
[more]
Contributed by: Roger J. Brown (March 2011)
Reproduced by permission of Academic Press from Private Real Estate Investment ©2005
Open content licensed under CC BY-NC-SA
Snapshots
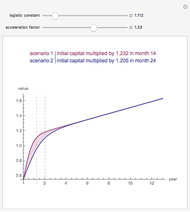
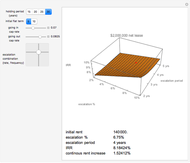
Details
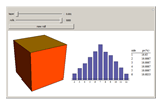
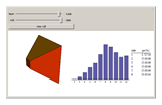
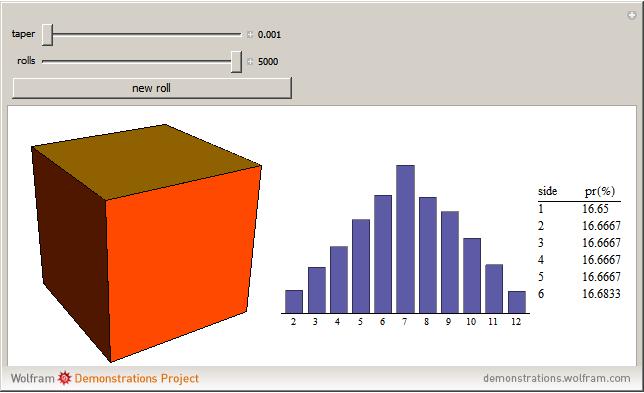
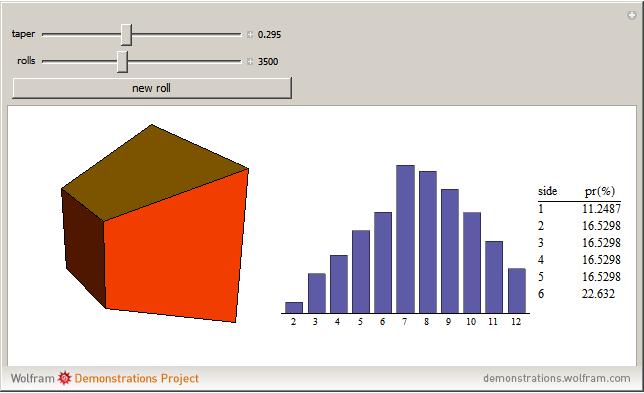
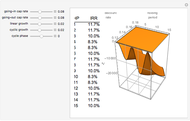
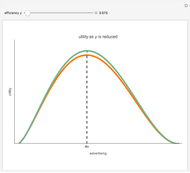
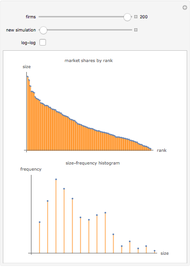
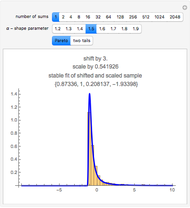
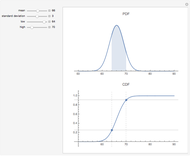
Note that as the taper increases, the probability for landing on the small end (side 1) declines and the probability for landing on the large end (side 6) increases. In this stylized example, the remaining four sides change very little. Repeated throws of a pair of such dice produce the outcome shown in the histogram. Note that in the initial case (the cube), the histogram is symmetrical, as expected. As the taper increases, the distribution becomes heavy on the right side. (In the limit, this produces a heavy right tail for the continuous case.)
Assumptions are the mother's milk of theory and this is no exception. For this to work the following must be true:
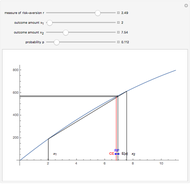
The data is a table of  integers that can only take the values of 2 through 12, inclusive, which arise from the following conditions: We have a pair of six-faced dice identical to each other, each with one to six pips on a side. The "sides" of each die are identical trapezoids but the "ends" are, of course, squares, the sizes of which differ with the increase of the taper. The taper variable determines the relative sizes of the "ends" as the cross section of the die tapers in a linear fashion along its original length. Assume in the deformation process that the volume of the die remains constant.
integers that can only take the values of 2 through 12, inclusive, which arise from the following conditions: We have a pair of six-faced dice identical to each other, each with one to six pips on a side. The "sides" of each die are identical trapezoids but the "ends" are, of course, squares, the sizes of which differ with the increase of the taper. The taper variable determines the relative sizes of the "ends" as the cross section of the die tapers in a linear fashion along its original length. Assume in the deformation process that the volume of the die remains constant.
Each face has a probability, based solely on its relative surface area, that it will come to rest on the table, revealing the payoff on the opposite side. It is expected that the largest side will (naturally) come to rest on the table most of the time, therefore its probability is the highest. The numeric output is a list of probabilities in which the "pips showing on the upside" payoff is in order of ascending payoff. That means that the smallest number of pips, 1, is on the large face of the dice, the one that is most likely to come to rest on the table. Thus, in that case it has the lowest probability and is represented by the first element in the list.
In order for the landing probabilities of such a die to depend solely on the relative area of its sides, assume that the die is statically and dynamically balanced about its center. This means, roughly, that both the first and second moments of mass distribution are equal with respect to any axes through the center. (Failing to require this introduces a nasty physics problem dealing with the other popular means of "loading" dice: adding weight to one side.)
More information is available in Chapter Six of Private Real Estate Investment and at mathestate.com.
R. J. Brown, Private Real Estate Investment: Data Analysis and Decision Making, Burlington, MA: Elsevier Academic Press, 2005.
Permanent Citation