Bootstrapping to Compute Value-at-Risk Standard Errors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
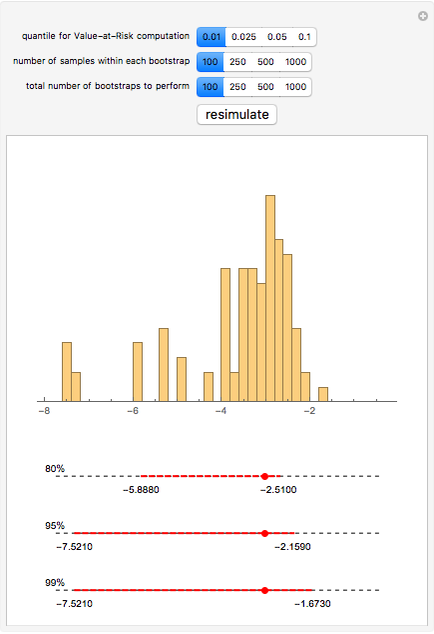
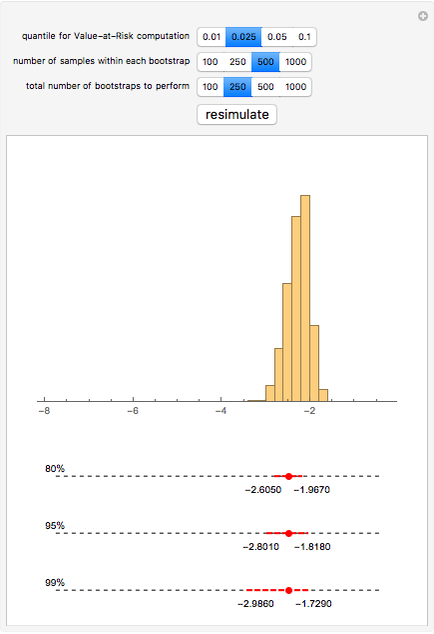
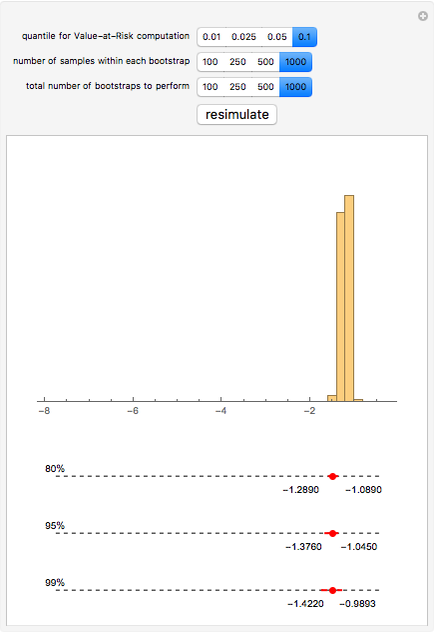
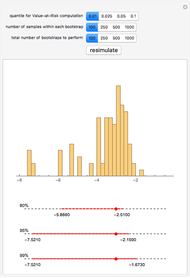
We obtain daily log-return data for the S&P 500 (with dividends reinvested) for the past twenty years, bootstrap low quantiles of the data, and then construct various confidence intervals around those estimated low quantiles. These low quantiles are related to a measure of risk called Value-at-Risk (VaR).
[more]
Contributed by: Jeff Hamrick (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
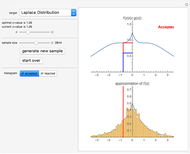
In some cases, VaR can be computed analytically—for example, if the portfolio's future value is assumed to be a log-normal random variable. The computation of VaR from historical data is equivalent to calculating a low quantile of the historical data (multiplied, perhaps, against a particular portfolio value to obtain a dollar value rather than a percentage loss figure). The resulting value is taken as an estimate of the true underlying VaR. Unfortunately, the standard errors of such an estimate depend on the underlying (and unknown) distribution of the returns. Bootstrapping is one methodology that is useful for estimating those standard errors.
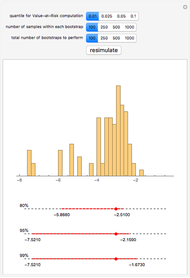
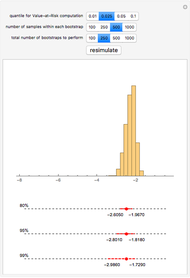
We show the following output: a histogram of the bootstrapped VaR values for a given input from the user. Additionally, we give 80%, 95%, and 99% bootstrapped confidence intervals around the point estimate of the VaR—the sample quantile of the daily log-return data for the S&P 500. This point estimate is shown as a large red dot.
Permanent Citation
"Bootstrapping to Compute Value-at-Risk Standard Errors"
http://demonstrations.wolfram.com/BootstrappingToComputeValueAtRiskStandardErrors/
Wolfram Demonstrations Project
Published: March 7 2011