Hodographs for Kepler Orbits

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
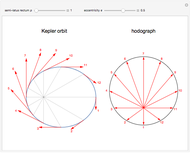
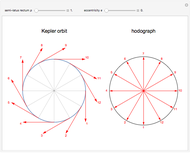
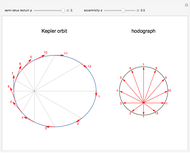
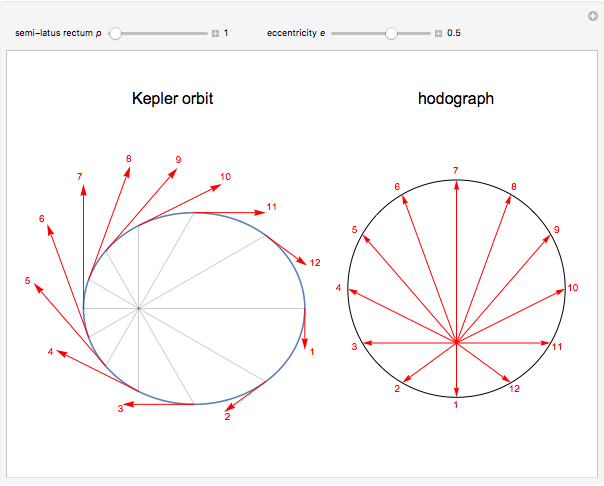
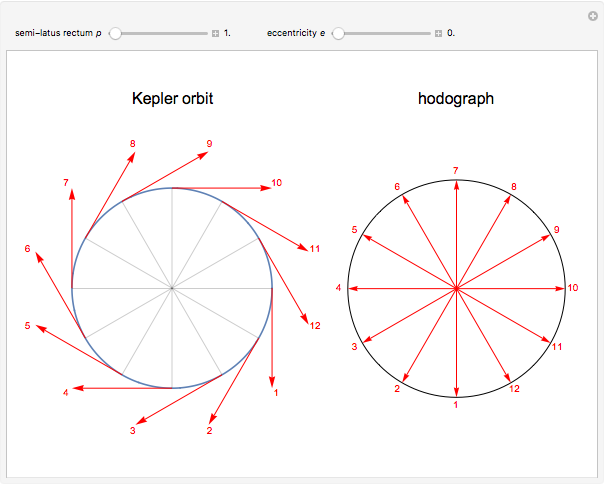
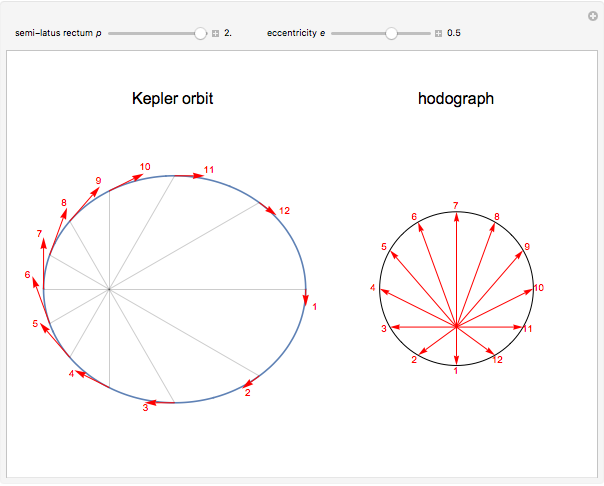
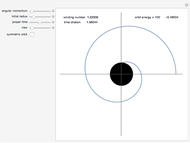
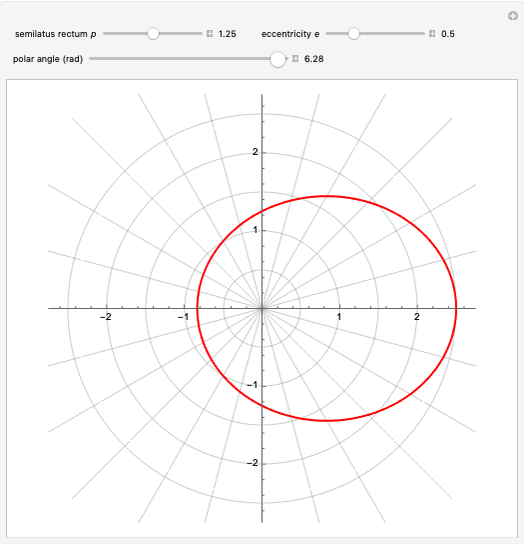
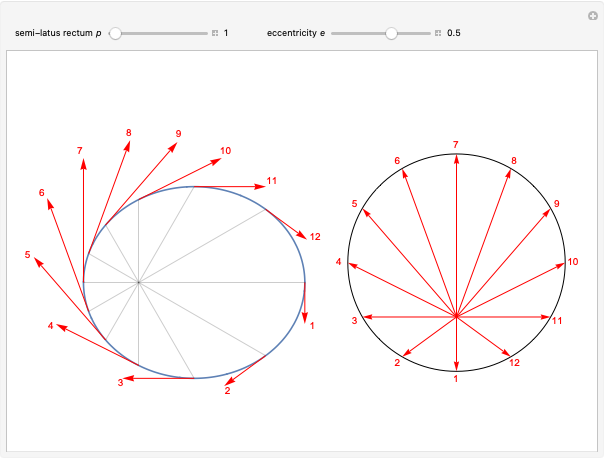
Kepler orbits are conic sections, most notably ellipses for stable periodic motion of a planet around the Sun. A lesser-known property is the motion of the associated tangential velocity vector, which traces out a circular orbit in velocity space. Hamilton (1864) first introduced the term hodograph to denote this motion.
[more]
Contributed by: S. M. Blinder (October 2019)
Open content licensed under CC BY-NC-SA
Details
The spherical components of velocity are converted to Cartesian coordinates using
 ,
,
 ,
,
 .
.
Taking the time derivative of the orbital formula above and using the angular-momentum definition
 ,
,
we obtain the Cartesian velocity components
 ,
,
 .
.
The relation
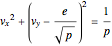
shows that the velocity vector traces out a circle of radius 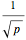 in velocity space centered at
in velocity space centered at  .
.
References
[1] E. I. Butikov, "The Velocity Hodograph for an Arbitrary Keplerian Motion," European Journal of Physics, 21(4), 2000 pp. 297–302. doi:10.1088%2F0143-0807%2F21%2F4%2F303.
[2] ThatsMaths. "Kepler’s Vanishing Circles Hidden in Hamilton’s Hodograph." (Oct 4, 2019) thatsmaths.com/2019/05/02/keplers-vanishing-circles-hidden-in-hamiltons-hodograph.
Snapshots
Permanent Citation