Zero-Energy Limit of Coulomb Wavefunctions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
In the limit of zero energy, the Coulomb–Schrödinger equation in atomic units simplifies to
[more]
Contributed by: S. M. Blinder (June 2019)
Open content licensed under CC BY-NC-SA
Details
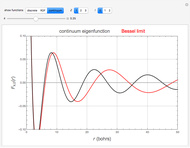
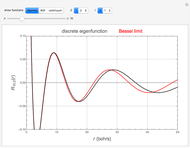
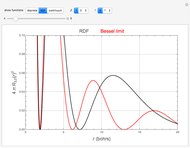
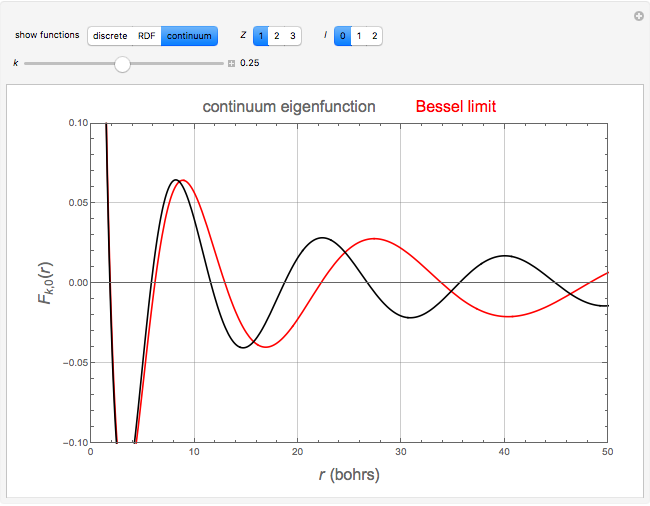
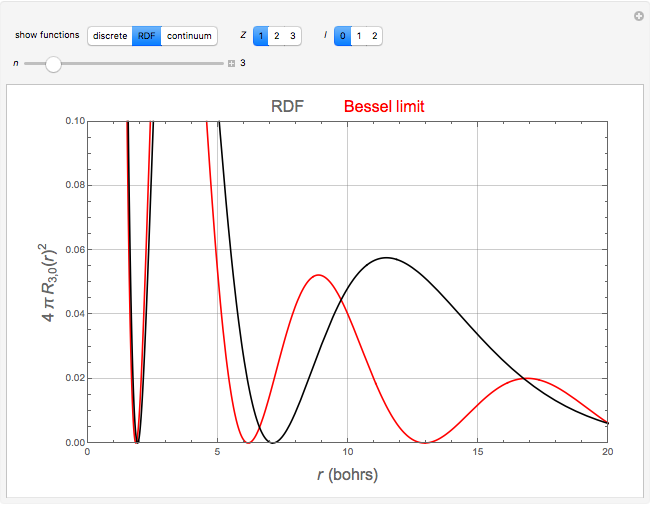
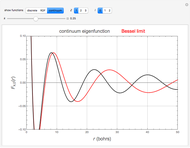
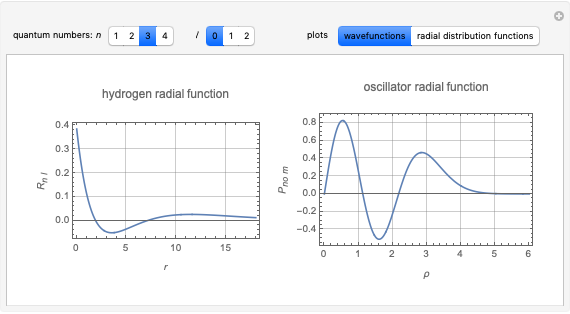
The hydrogenic eigenfunctions, expressed in terms of confluent hypergeometric functions  , are given in [1]. The normalization constants are trimmed so as to coincide with the Bessel function limit as
, are given in [1]. The normalization constants are trimmed so as to coincide with the Bessel function limit as  for the discrete eigenfunctions and
for the discrete eigenfunctions and  for the continuum. Thus we take
for the continuum. Thus we take

and

for the discrete and continuum eigenfunctions, respectively.
The limiting behavior as  or
or  can be deduced from the asymptotic limit [2]:
can be deduced from the asymptotic limit [2]:

as  .
.
References
[1] H. A. Bethe and E. E. Salpeter, Quantum Mechanics of One- and Two-Electron Atoms, New York: Academic Press, 1957 pp. 21–25.
[2] "Confluent Hypergeometric Functions." NIST Digital Library of Mathematical Functions. (Jun 18, 2019) dlmf.nist.gov/13.8.E9.
Snapshots
Permanent Citation