Wolfram Demonstrations Project

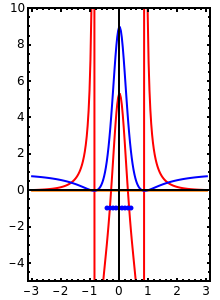
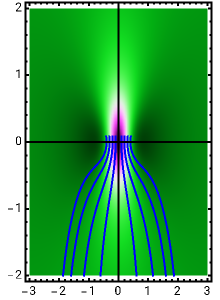
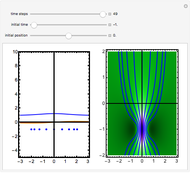
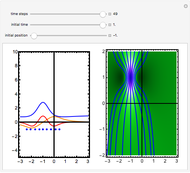
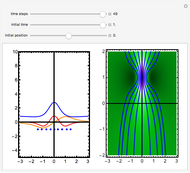
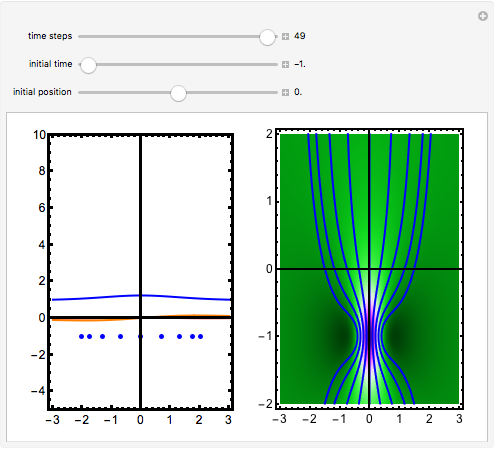
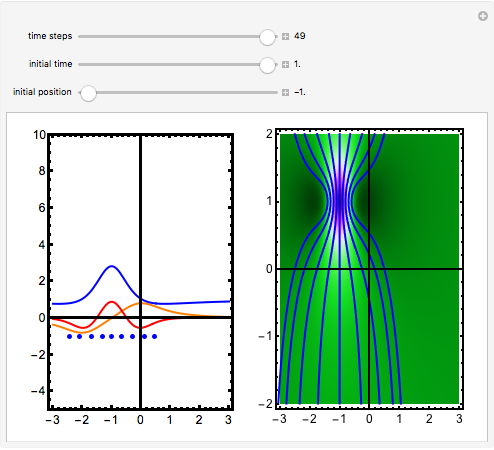
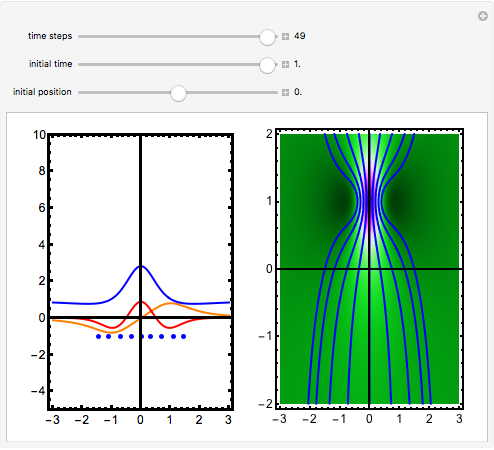
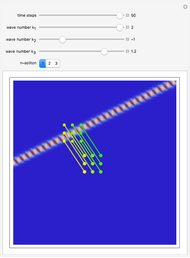
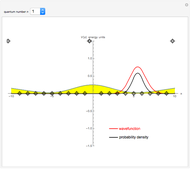
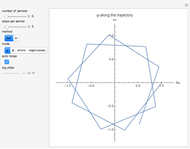
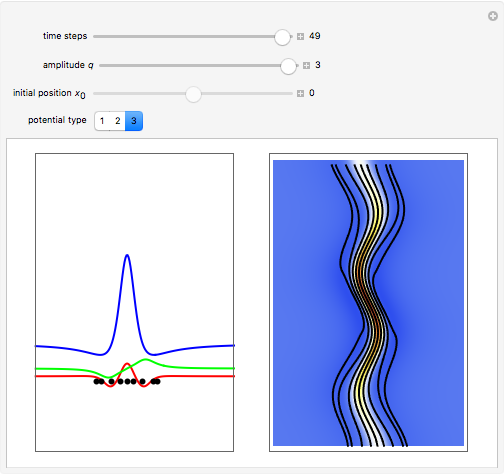
The standard "self-focusing" nonlinear Schrödinger equation, also known as the Gross–Pitaevskii equation, appears in wave propagation through nonlinear media such as signal transmission in optical fibers, Bose–Einstein condensation, and surface waves over sufficiently deep water. This Demonstration studies a spatially localized algebraic breather solution (Peregrine soliton), where the maximum of the squared wavefunction varies by initial conditions. The causal interpretation of quantum theory developed by Louis de Broglie and David Bohm introduced trajectories that are guided by a quantum potential. The velocities of single particles, following the trajectories, are determined by the phase of the wavefunction. The system is time reversible.

In the graphic on the left, you can see the position of the particles (blue), the squared wavefunction (blue), the quantum potential (red), and the velocity (orange). On the right, the graphic shows the squared wavefunction plus trajectories.

Contributed by: Klaus von Bloh

Gamepad Controls
Automatic Animation

The nonlinear Schrödinger equation is

, with

, and so on, where

is a complex function and

is its complex conjugate. Here the common standard notation is used, where

is the temporal and

is the spatial coordinate. The maximum of the original Peregrine soliton is located at the fixed point

[1]. Wang, He, and Li find in [2] a rational-like solution with a controllable center, which has the same structure as the original Peregrine breather solution.

In the eikonal representation of the wave,

, the gradient of the phase

is the particle velocity

. In this interpretation, the origin of the motion of the particle is the potential

, given by

, plus an additional term

. The latter may be interpreted alternatively as a kind of fluid pressure or quantum potential.

For the complex-valued wavefunction,

there is an analytic solution for the quantum motion, where the squared modulus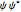

of the wavefunction is interpreted as the wave density. The phase function

for the breather is defined as

from which the equation of motion is derived by solving:

The analytical solution is given, where

is an integration constant. The initial position is estimated by solving the equation

numerically. Real-valued trajectories are obtained for several

's. The starting positions of the particles are linearly distributed around the peak of the wave at

and

. You can control the paths together with the starting points by changing the initial conditions

and

. The path

together with the starting point leads to a trajectory in

space.

References

[1] D. H. Peregrine, "Water Waves, Nonlinear Schrödinger Equations and Their Solutions," Journal of the Australian Mathematical Society, Series B, 25(1), 1983 pp. 16–43. journals.cambridge.org/action/displayAbstract?fromPage=online&aid=3968224.

[2] X.-C. Wang, J.-S. He, and Y.-S. Li, "Rogue Wave with a Controllable Center of Nonlinear Schrödinger Equation," Communications in Theoretical Physics, 56(4), 2011 pp. 631–637. ctp.itp.ac.cn/EN/volumn/volumn_1277.shtml.

Quantum Mechanics (ScienceWorld)

Schrödinger Equation (ScienceWorld)

Klaus von Bloh

"Peregrine Soliton with Controllable Center in the Causal Interpretation of Quantum Mechanics"
http://demonstrations.wolfram.com/PeregrineSolitonWithControllableCenterInTheCausalInterpretat/
Wolfram Demonstrations Project
Published: November 17, 2011