Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Inverted Pendulum Controls

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

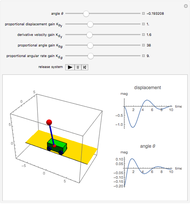
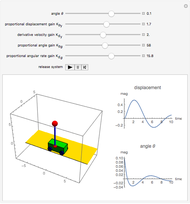
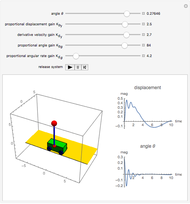
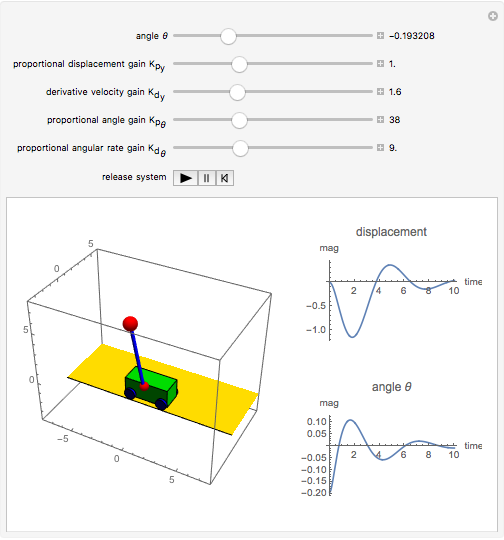
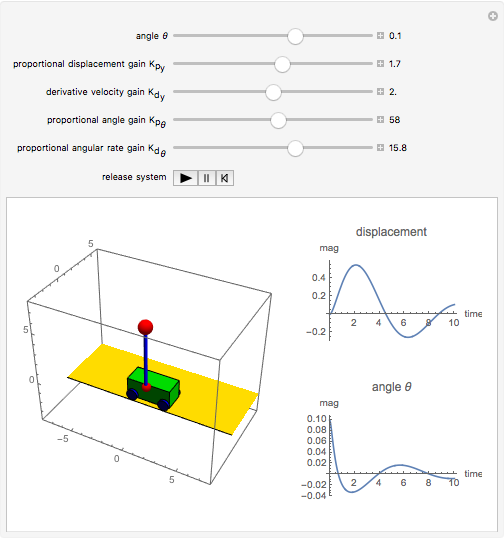
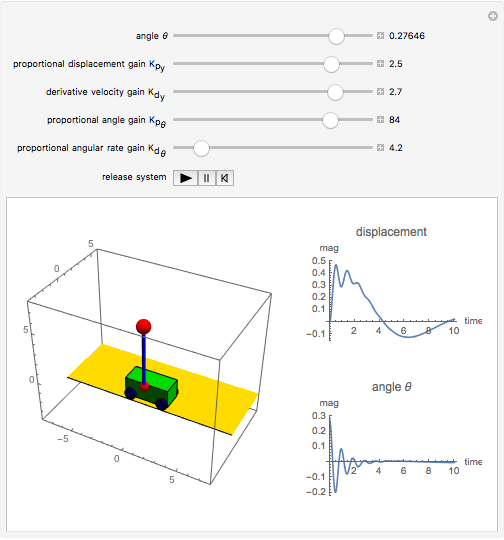
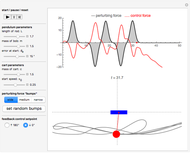
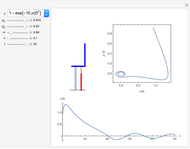
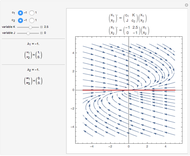
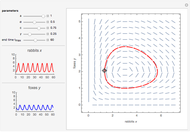
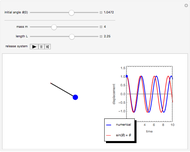
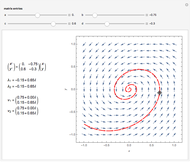
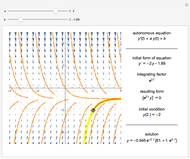
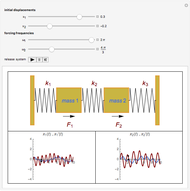
The problem is to move the cart supporting a rod so that the rod does not fall, or—even better—so that the rod stays vertical. This classic problem appears in the control of the Segway invented by Dean Kamen. The solution shown here uses a proportional derivative controller. Other parameters can be examined using this example, but at some point it becomes too complicated for a simple visualization. You can vary several parameters to demonstrate the stability of the device, which can be instructive. The problem includes free body diagrams and variables that can be included in future versions.

Contributed by: Stephen Wilkerson (Towson University) and Nathan Slegers (University of Alabama, Huntsville) with contributions by Franz Brandhuber (March 2011)
Open content licensed under CC BY-NC-SA

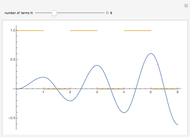
Snapshots

Details

Here are the equations used:

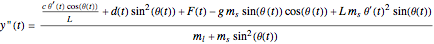
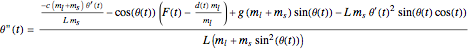
Control law:

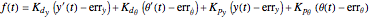
glossary of terms:

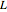is the length of the pendulum

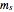is the small mass on top of the pendulum

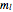is the mass of the sled

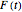is the force applied to the sled to keep the pendulum in the vertical position

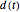is the force on the small mass (here 0)

is the rotation of the pendulum

is the rotation rate of the pendulum

is the rotational acceleration of the pendulum

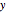is the displacement of the sled

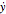is the velocity of the sled

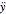is the acceleration of the sled

is the acceleration due to gravity

is the angular damping of inverted pendulum shaft

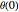is the initial angle of the pendulum

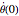is the initial angle rate assumed as zero

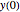is the initial displacement of the sled assumed at zero

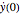is the initial velocity of the sled assumed at zero

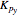is the proportional displacement gain

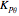is the proportional angle gain

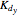is the derivative displacement gain

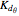is the derivative angle gain

Permanent Citation

Stephen Wilkerson (Towson University) and Nathan Slegers (University of Alabama, Huntsville) with contributions by Franz Brandhuber "Inverted Pendulum Controls"
http://demonstrations.wolfram.com/InvertedPendulumControls/
Wolfram Demonstrations Project
Published: March 7 2011

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send