Transformation to Symmetry of Gamma Random Variables

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
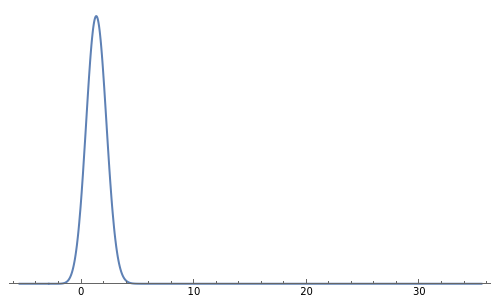
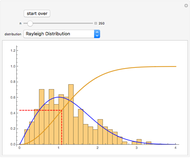
This Demonstration shows the probability density function for the transformed random variable,  :
:
Contributed by: Ian McLeod and Nagham Muslim Mohammad (June 2013)
(Department of Statistical and Actuarial Sciences, Western University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: The scale parameter  has been increased from
has been increased from  in the thumbnail to
in the thumbnail to  . There no change in the symmetry.
. There no change in the symmetry.
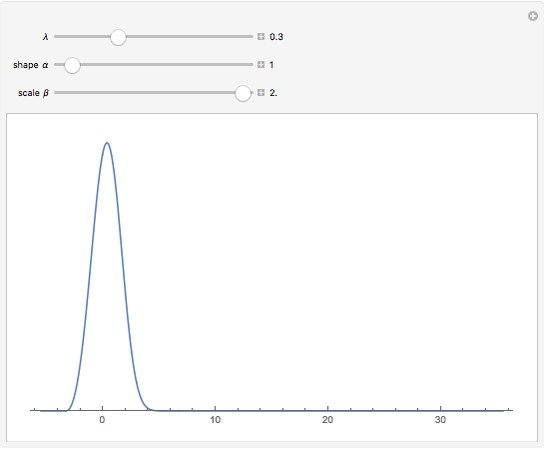
Snapshot 2: Here  , so this corresponds to the standard unit exponential distribution. Because of the Box–Cox transformation with
, so this corresponds to the standard unit exponential distribution. Because of the Box–Cox transformation with  , the location has been shifted to the left by 1, so the mean of the resulting distribution is now 0, while the variance remains at 1.
, the location has been shifted to the left by 1, so the mean of the resulting distribution is now 0, while the variance remains at 1.
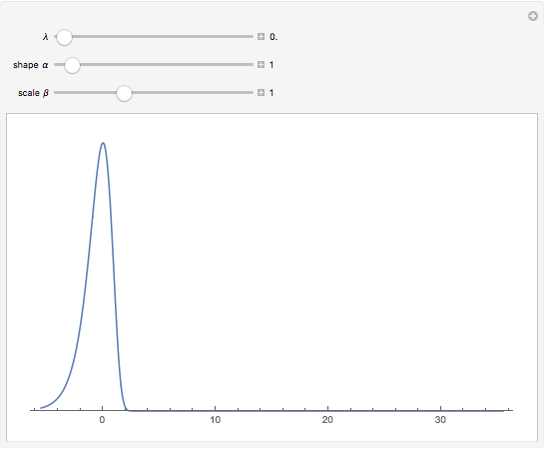
Snapshot 3: The logarithmic transformation,  , for the exponential distribution is shown. Comparing with
, for the exponential distribution is shown. Comparing with  in the case shown in the caption, we see that
in the case shown in the caption, we see that  does better. As an exercise, you might like to compute the skewness coefficient,
does better. As an exercise, you might like to compute the skewness coefficient,  , where
, where  and
and  are the second and third moments of the transformed distribution. The skewness coefficients for selected values of
are the second and third moments of the transformed distribution. The skewness coefficients for selected values of  are shown in the table below:
are shown in the table below:

The built-in Mathematica function FindRoot found that  for
for  .
.
Snapshot 4: When the shape parameter increases, the gamma distribution approximates the normal. Here  and
and  corresponds to no transformation, apart from a shift in location, and even with
corresponds to no transformation, apart from a shift in location, and even with  , the gamma distribution is close to the normal distribution. The degree of approximation could be visualized using normal quantile or probability plots. You may be interested in extending this Demonstration to include the use of these plots for choosing a suitable transformation.
, the gamma distribution is close to the normal distribution. The degree of approximation could be visualized using normal quantile or probability plots. You may be interested in extending this Demonstration to include the use of these plots for choosing a suitable transformation.
The theory of variance-stabilizing transformations was derived in [1]. For more details and examples with transformation to symmetry of random variables, see [2].
References
[1] M. S. Bartlett, "The Use of Transformations," Biometrics, 3(1), 1947 pp. 37–52.
[2] I. McLeod. "Symmetrizing Positive Random Variables" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/SymmetrizingPositiveRandomVariables.
Permanent Citation