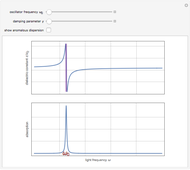
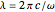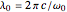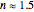Lorentz Oscillator Model for Refractive Index

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
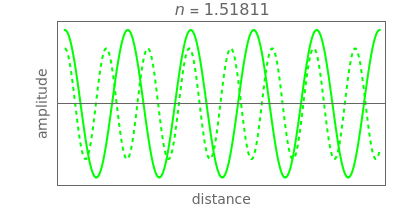
The index of refraction  is often described as an apparent decrease in the speed of light from
is often described as an apparent decrease in the speed of light from  to
to 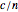 as it passes through a dielectric medium. In fact, light photons do not actually slow down, but the effect is simulated by a retarding phase shift in the emerging electromagnetic waves. This is caused by superposition of the incident wave with a retarded wave produced by radiation from the electrons in the medium.
as it passes through a dielectric medium. In fact, light photons do not actually slow down, but the effect is simulated by a retarding phase shift in the emerging electromagnetic waves. This is caused by superposition of the incident wave with a retarded wave produced by radiation from the electrons in the medium.
Contributed by: S. M. Blinder (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
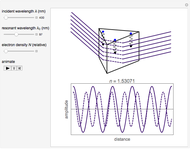
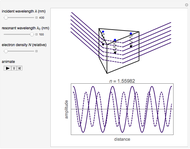
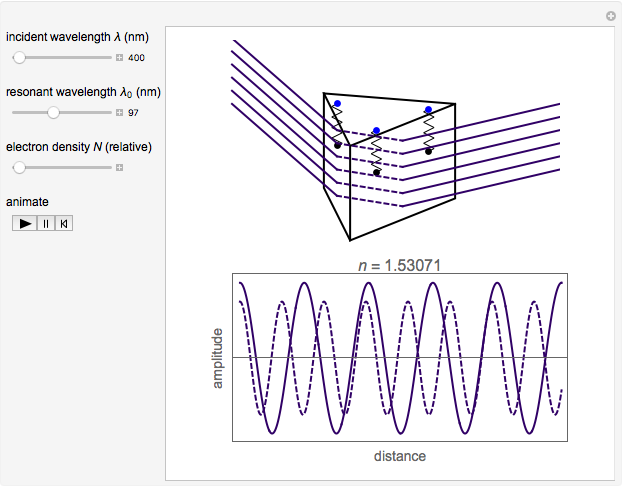
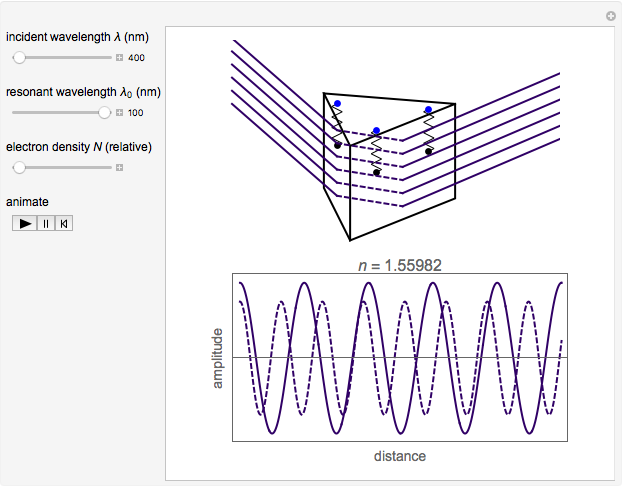
Assume a monochromatic plane electromagnetic wave incident on a transparent dielectric. It is sufficient to consider just the electric field component, represented by 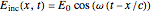 , propagating in the
, propagating in the  direction and polarized in the
direction and polarized in the  direction. It is convenient to do computations with the corresponding complex forms, such as
direction. It is convenient to do computations with the corresponding complex forms, such as 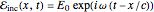 . Assume that the polarizable electrons in the medium can be represented by Lorentz oscillators—classical charged harmonic oscillators, governed by the equation of motion
. Assume that the polarizable electrons in the medium can be represented by Lorentz oscillators—classical charged harmonic oscillators, governed by the equation of motion 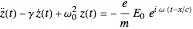 , distributed throughout the medium. Here
, distributed throughout the medium. Here  and
and 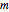 are the charge and mass of the electron,
are the charge and mass of the electron, 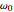 is the fundamental frequency of the oscillator, and
is the fundamental frequency of the oscillator, and  is a damping constant associated with the loss of energy by radiation. Assume that
is a damping constant associated with the loss of energy by radiation. Assume that 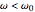 , such that, for a transparent medium, when
, such that, for a transparent medium, when  lies in the visible region,
lies in the visible region, 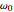 is in the ultraviolet. The steady-state solution to the equation of motion reduces to
is in the ultraviolet. The steady-state solution to the equation of motion reduces to  [1]. The corresponding electric current is given by
[1]. The corresponding electric current is given by  and the current density by
and the current density by 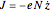 , where
, where 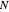 is the number of oscillating electrons per unit volume (typically of the order of
is the number of oscillating electrons per unit volume (typically of the order of 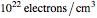 ).
).
To determine the radiation field produced by the collection of oscillators, we require 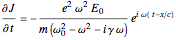 . The electric field of the radiation is then satisfied by a wave equation
. The electric field of the radiation is then satisfied by a wave equation 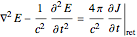 , which pertains to the
, which pertains to the  components of
components of 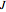 and
and 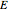 as functions of
as functions of  and
and  . The subscript
. The subscript 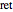 indicates that
indicates that 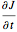 is to be evaluated at retarded times, taking account of the transmission from source points to field points at the speed of light,
is to be evaluated at retarded times, taking account of the transmission from source points to field points at the speed of light,  . Retardation can be accounted for very simply by replacing
. Retardation can be accounted for very simply by replacing 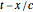 in the phase factor by
in the phase factor by 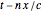 , where
, where 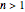 (
( will turn out to equal the index of refraction). The steady-state, far-field solution to the wave equation can be obtained by assuming that
will turn out to equal the index of refraction). The steady-state, far-field solution to the wave equation can be obtained by assuming that 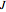 and
and 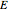 both have phase factors
both have phase factors 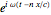 . This leads to an expression for the radiation field
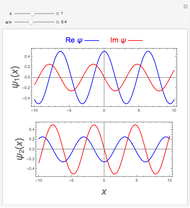
. This leads to an expression for the radiation field  , with the index of refraction given by
, with the index of refraction given by 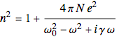 (for SI units, replace
(for SI units, replace 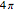 by
by  ). When
). When 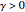 , the medium exhibits some absorption of the incident radiation. This can make the index of refraction a complex quantity,
, the medium exhibits some absorption of the incident radiation. This can make the index of refraction a complex quantity, 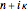 , with the transmitted amplitude attenuated by a factor
, with the transmitted amplitude attenuated by a factor 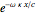 . The effect is generally small and we neglect it.
. The effect is generally small and we neglect it.
References
[1] H. A. Lorentz, The Theory of Electrons and Its Applications to the Phenomena of Light and Radiant Heat, New York: Dover Books, 2011 (original 1915).
[2] J. D. Jackson, Classical Electrodynamics, 3rd ed., New York: John Wiley & Sons, 1999 pp. 246, 309–310ff.
[3] R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics, Vol. 2, Reading, MA: Addison–Wesley, 1964 Chap. 32.
Permanent Citation